
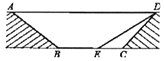
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
【答案】(1)7.4米;(2)(8+3![]() -3
-3![]() )米
)米
【解析】试题分析: (1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,根据已知得出DM=CM=![]() CD=3
CD=3![]() ,则AN=DM=3
,则AN=DM=3![]() ,再解Rt△ANB,由通道斜面AB的坡度i=1:
,再解Rt△ANB,由通道斜面AB的坡度i=1: ![]() ,得出BN=
,得出BN=![]() AN=6,然后根据勾股定理求出AB;
AN=6,然后根据勾股定理求出AB;
(2)先解Rt△MED,求出EM=![]() DM=3
DM=3![]() ,得出EC=EM-CM=3
,得出EC=EM-CM=3![]() -3
-3![]() ,再根据BE=BC-EC即可求解.
,再根据BE=BC-EC即可求解.
试题解析:(1)过点A作AN⊥CB于点N,过点D作DM⊥BC于点M,
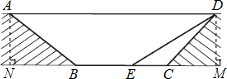
∵∠BCD=135°,
∴∠DCM=45°.
∵在Rt△CMD中,∠CMD=90°,CD=6,
∴DM=CM=![]() CD=3
CD=3![]() ,
,
∴AN=DM=3![]() ,
,
∵通道斜面AB的坡度i=1: ![]() ,
,
∴tan∠ABN=![]() ,
,
∴BN=![]() AN=6,
AN=6,
∴AB=![]() =3
=3![]() ≈7.4.
≈7.4.
即通道斜面AB的长约为7.4米;
(2)∵在Rt△MED中,∠EMD=90°,∠DEM=30°,DM=3![]() ,
,
∴EM=![]() DM=3
DM=3![]() ,
,
∴EC=EM-CM=3![]() -3
-3![]() ,
,
∴BE=BC-EC=8-(3![]() -3
-3![]() )=(8+3
)=(8+3![]() -3
-3![]() )米
)米


科目:初中数学 来源: 题型:
【题目】如图,点P与点Q都在y轴上,且关于x轴对称.
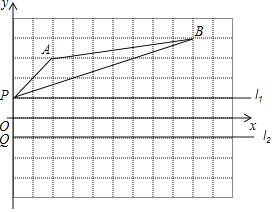
(1)请画出△ABP关于x轴的对称图形△A′B′Q(其中点A的对称点用A′表示,点B的对称点用B′表示);
(2)点P、Q同时都从y轴上的位置出发,分别沿l1、l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得AP+BQ=A′B成立?若存在,请你在图中画出此时PQ的位置(用线段P′Q′表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:二元一次方程![]() 有无数组解,每组解记为
有无数组解,每组解记为![]() ,称
,称![]() 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
(1) 已知![]() ,则是隐线
,则是隐线![]() 的亮点的是 ;
的亮点的是 ;
(2) 设![]() 是隐线
是隐线![]() 的两个亮点,求方程
的两个亮点,求方程![]() 中
中![]() 的最小的正整数解;
的最小的正整数解;
(3)已知![]() 是实数, 且
是实数, 且![]() ,若
,若![]() 是隐线
是隐线![]() 的一个亮点,求隐线
的一个亮点,求隐线![]() 中的最大值和最小值的和.
中的最大值和最小值的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长青农产品加工厂与 A,B 两地有公路、铁路相连.这家工厂从 A 地购买一批原料甲运回工厂,经过加工后制成产品乙运到 B 地,其中原料甲和产品乙的重量都是正整数.
已知铁路运价为 2 元/(吨·千米),公路运价为 8 元/(吨·千米).

(1)若由 A 到 B 的两次运输中,原料甲比产品乙多 9 吨,工厂计划支出铁路运费超 过 5700 元,公路运费不超过 9680 元.问购买原料甲有哪几种方案,分别是多少吨?
(2)由于国家出台惠农政策,对运输农产品的车辆免收高速通行费,并给予一定的 财政补贴,综合惠农政策后公路运输价格下降 m( 0 m 4 且 m 为整数)元, 若由 A 到 B 的两次运输中,铁路运费为 5760 元,公路运费为 5100 元,求 m 的 值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作AC的垂直平分线,交AB于点O,交AC于点D;
②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)在(1)所作的图形中,解答下列问题.
①点B与⊙O的位置关系是__;(直接写出答案)
②若DE=2,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,AC交⊙O于点E,BC交⊙O于点D,F为CE的中点,连接DF.给出以下五个结论:①BD=DC;②AD=2DF;③ ![]() ;④DF是⊙O的切线.其中正确结论的个数是:( )
;④DF是⊙O的切线.其中正确结论的个数是:( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com