
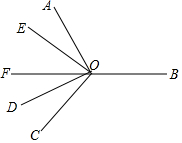
 如图,在平面内,∠AOB=∠COB,∠AOD=∠COE=90°,OF平分∠DOE,则以下结论:
如图,在平面内,∠AOB=∠COB,∠AOD=∠COE=90°,OF平分∠DOE,则以下结论:分析 根据角平分线的性质可得∠EOF=∠DOF,根据等角的补角相等得到∠BOE=∠BOD,即可判断①正确;
由∠AOC=∠AOE+∠COE=∠AOE+90°,∠DOE=∠AOD-∠AOE=90°-∠AOE,可得∠AOC+∠DOE=180°,即可判断②正确;
由∠AOC-∠DOE=∠AOE+90°-∠DOE,而∠AOE≠∠DOE,即可判断③不正确;
由①可知∠BOE=∠BOD,又∠AOB=∠COB,所以∠AOE=∠COD,由OF平分∠DOE得∠EOF=∠DOF,那么∠AOF=∠COF,进而判断④正确.
解答 解:(1)①②④正确.
故答案为①②④;
(2)如果选择①.
∵OF平分∠DOE,
∴∠EOF=∠DOF,
∴∠BOE=∠BOD;
如果选择②.
∵∠AOC=∠AOE+∠COE=∠AOE+90°,∠DOE=∠AOD-∠AOE=90°-∠AOE,
∴∠AOC+∠DOE=∠AOE+90°+90°-∠AOE=180°;
如果选择④.
∵∠BOE=∠BOD,∠AOB=∠COB,
∴∠AOE=∠COD,
∵OF平分∠DOE,
∴∠EOF=∠DOF,
∴∠AOF=∠COF,
∴∠AOB+∠COF=180°.
点评 本题考查了余角和补角,角度的计算,余角的性质,角平分线的定义,准确识图是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 应试者 | 测试成绩 | ||
| 创新能力 | 计算机能力 | 公关能力 | |
| 甲 | 72 | 50 | 88 |
| 乙 | 85 | 74 | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 85 | 88 | 84 | 85 | 83 |
| 乙 | 83 | 87 | 84 | 86 | 85 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com