
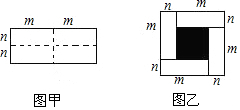
 已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.分析 (1)第一种方法为:大正方形面积-4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(2)根据图形即可得到结论;
(3)利用(a-b)2=(a+b)2-4ab可求解.
解答 解:(1)(m+n)2-4mn或(m-n)2;
故答案为:(m+n)2-4mn,(m-n)2;
(2)(m+n)2-4mn=(m-n)2;
故答案为:(m+n)2-4mn=(m-n)2;
(3)∵(a-b)2=(a+b)2-4ab,
∵a+b=8,ab=5,
∴(a-b)2=64-20=44.
∴a-b=±2$\sqrt{11}$.
点评 本题主要考查了完全平方式的知识,解决问题的关键是读懂题意,找到所求的量的等量关系.本题更需注意要根据所找到的规律做题.


科目:初中数学 来源: 题型:解答题
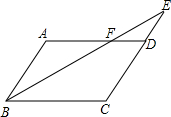 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{7}{4}$ | C. | $\frac{8\sqrt{10}}{3}$ | D. | $\frac{28}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
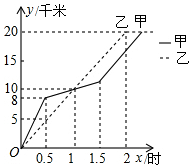 在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:
在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com