
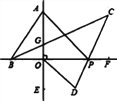
【题目】如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,
AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.
(1)求∠BGO的度数;
(2)试确定∠C与∠OAP之间的数量关系,并说明理由;
(3)P在直线上运动,∠C+∠D的值是否变化?若发生变化,说明理由;若不变求其值.
【答案】(1)60° ;(2)见解析; (3)∠C+∠D不变 ,理由见解析。
【解析】试题分析:(1)根据已知求出∠ABG的度数,运用外角的性质求出∠BGO的度数;
(2)根据外角的性质表示出∠C,得到∠C与∠OAP之间的数量关系;
(3)根据对顶角相等,分别表示出∠C和∠D,得到∠C+∠D的值.
试题解析:解:(1)∵∠BAO=30°,∴∠ABO=60°.∵BC平分∠ABP,∴∠ABG=∠GBO=30°,∠BGO=∠BAG+∠ABG=60°.
(2)∠C=![]() ∠OAP+15°.理由如下:
∠OAP+15°.理由如下:
∠APF=∠OAP+∠AOP,∠C=![]() ∠APF﹣∠CBF=
∠APF﹣∠CBF=![]() ∠OAP+45°﹣30°=
∠OAP+45°﹣30°=![]() ∠OAP+15°.
∠OAP+15°.
(3)∠C+∠D不变.理由如下:
∵∠CPF=∠OPD,∠CPF=∠C+30°,∠OPD=180°﹣45°﹣∠D,∴∠C+30°=180°﹣45°﹣∠D,∴∠C+∠D=105°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
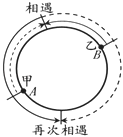
【题目】如图,在一圆形跑道上,甲从A点、乙从B点同时出发,反向而行,8分钟后两人相遇,再过6分钟甲到B点,又过10分钟两人再次相遇.甲环行一周需要的时间是( )
A. 26分钟 B. 28分钟 C. 30分钟 D. 32分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.
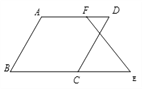
求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD ( )
∴∠B=_______( )
又∵∠B=∠D(已知 ),
∴∠D=_______( )
∴AD∥BE( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
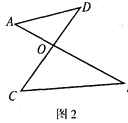
【题目】如图,图1是△ABC,图2是“8字形”(将线段AB、CD相交于点O,连接AD、CB形成的图形),图3是一个五角星形状,试解答下列问题:

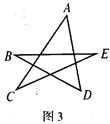
(1)图1的△ABC中,∠A+∠B+∠C=_____,并证明你写出的结论;(要有推理证明过程)
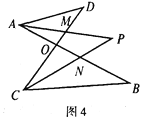
(2)图2的“8字形”中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:_____;
(3)若在图2的条件下,作∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N(如图4).请直接写出∠P与∠D、∠B之间数量关系:____;
(4)图3中的点A向下移到线段BE上时,请直接写出∠CAD+∠B+∠C+∠D+∠E=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有_____个白球.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com