
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限,
在第一象限,![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() .
.
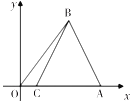
(1)求证:![]() ;
;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)cos∠ABO=![]()
【解析】
(1)过点![]() 作
作![]() 点
点![]() ,在
,在![]() 中,利用锐角三角函数的知识求出BD的长,再用勾股定理求出OD、AB、BC的长, 所以AB=BC,从而得到∠ACB=∠BAO,然后根据两角分别相等的两个三角形相似解答即可;
中,利用锐角三角函数的知识求出BD的长,再用勾股定理求出OD、AB、BC的长, 所以AB=BC,从而得到∠ACB=∠BAO,然后根据两角分别相等的两个三角形相似解答即可;
(2)在![]() 中求出∠BAO的余弦值,根据∠ABO=∠BAO可得答案.
中求出∠BAO的余弦值,根据∠ABO=∠BAO可得答案.
(1)在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() ,
,
![]() ,∠OAB=∠ABO,
,∠OAB=∠ABO,
过点![]() 作
作![]() 点
点![]() ,
,
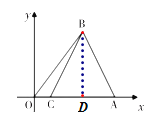
则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴CD=6-2=4,
∴BC=![]() ,
,
∴AB=BC,
∴∠ACB=∠BAO,
∴∠ACB=∠ABO=∠BAO,
又∵∠BAC=∠OAB,
![]() (两角分别相等的两个三角形相似);
(两角分别相等的两个三角形相似);
(2)在![]() 中,
中,
![]() ,
,
∵∠ABO=∠BAO ,
![]() ,
,
即![]() 的值为
的值为![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC、AB相交于点D、E,连接AD,已知∠CAD=∠B.
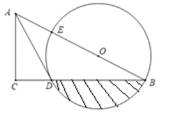
(1)求证:AD是⊙O的切线;
(2)若∠B=30°,AC=![]() ,求劣弧BD与弦BD所围阴影图形的面积;
,求劣弧BD与弦BD所围阴影图形的面积;
(3)若AC=4,BD=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图1).数学兴趣小组的小亮同学在塔上观景点P处,利用测角仪测得运河两岸上的A,B两点的俯角分别为17.9°,22°,并测得塔底点C到点B的距离为142米(A、B、C在同一直线上,如图2),求运河两岸上的A、B两点的距离(精确到1米).(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin17.9°≈0.31,cos17.9°≈0.95,tan17.9°≈0.32)
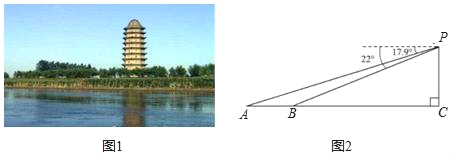
查看答案和解析>>
科目:初中数学 来源: 题型:
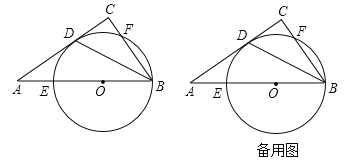
【题目】如图,在直角△ABC中,∠C=90°,AB=5,作∠ABC的平分线交AC于点D,在AB上取点O,以点O为圆心经过B、D两点画圆分别与AB、BC相交于点E、F(异于点B).
(1)求证:AC是⊙O的切线;
(2)若点E恰好是AO的中点,求![]() 的长;
的长;
(3)若CF的长为![]() ,①求⊙O的半径长;②点F关于BD轴对称后得到点F′,求△BFF′与△DEF′的面积之比.
,①求⊙O的半径长;②点F关于BD轴对称后得到点F′,求△BFF′与△DEF′的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() 且开口向下,则下列结论:①抛物线经过点
且开口向下,则下列结论:①抛物线经过点![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 有两个不相等的实数根;④对于任意实数
有两个不相等的实数根;④对于任意实数![]() ,
,![]() 总成立。其中结论正确的个数为( )
总成立。其中结论正确的个数为( )
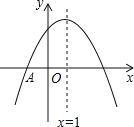
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确( )
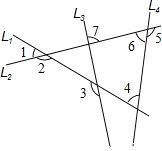
A. ∠2=∠4+∠7 B. ∠3=∠1+∠6 C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com