练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．同时投掷两枚硬币，出现两枚都是反面朝上的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{4}$C．1D．$\frac{3}{4}$

    分析 首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两枚都出现反面朝上的情况，再利用概率公式即可求得答案．

    解答 解：根据题意画树状图如下：

    ∵共有4种等可能的结果，两枚都出现反面朝上的有1种情况，
    ∴两枚都出现反面朝上的概率是$\frac{1}{4}$；
    故选B．

    点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．如图，菱形ABCD的面积为60cm2，则正方形AECF和正方形BGDH的面积之和的最小值为120cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．若m2=n2，则m=n，这个命题正确吗？试举例说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：
    （1）3$\sqrt{3}$×$\sqrt{3}$；（2）$\sqrt{0.5}$×$\sqrt{24}$；（3）$\sqrt{45}$×$\frac{3}{2}$$\sqrt{\frac{2}{3}}$；
    （4）-$\frac{1}{2}$$\sqrt{xy}$×（-4$\sqrt{y}$）；（5）-$\frac{4}{3}$$\sqrt{18}$÷2$\sqrt{8}$×$\frac{1}{3}$$\sqrt{54}$；（6）-2$\sqrt{xy}$÷（-$\frac{3}{2x}\sqrt{{x}^{2}y}$×3$\sqrt{x}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．由表的对应值知，一元二次方程ax2+bx+c=0（a，b，c为常数，a≠0）的一个根的百分位上的数字是4．
     x 3.23 3.24 3.25 3.26
     ax2+bx+c-0.06-0.02 0.030.09

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

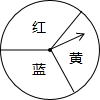    12．如果身边没有质地均匀的硬币，下列方法可以模拟掷硬币实验的是（　　）
    A．掷一个瓶盖，盖面朝上代表正面，盖面朝下代表反面
    B．掷一枚图钉，钉尖着地代表正面，钉帽着地代表反面
    C．掷一枚质地均匀的骰子，奇数点朝上代表正面，偶数点朝上代表反面
    D．转动如图所示的转盘，指针指向“红”代表正面，指针指向“蓝”代表反面

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．若4xmy3+（-2x2yn）=2xmyn，则nm=9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

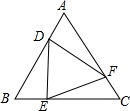    16．如图，等边△ABC中，点D，E，F分别同时从点A，B，C出发，以相同的速度在AB，BC，CA上运动，连结DE，EF，DF．
    （1）证明：△DEF是等边三角形；
    （2）在运动过程中
    ①若△CEF是等边三角形，试求$\frac{{S}_{△DEF}}{{S}_{△ABC}}$的值；
    ②试问△CEF有可能是直角三角形吗？若有，请求出$\frac{{S}_{△DEF}}{{S}_{△ABC}}$的值；若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．请你观察：
    $\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$；$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$；…
    $\frac{1}{1×2}$+$\frac{1}{2×3}$=$\frac{1}{1}$-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$=1-$\frac{1}{3}$=$\frac{2}{3}$；
    $\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=$\frac{1}{1}$-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$；…
    以上方法称为“裂项相消求和法”
    请类比完成：
    （1）$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$=$\frac{4}{5}$；
    （2）$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{2016×2017}$=$\frac{2016}{2017}$．
    （3）计算：$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$+$\frac{1}{9×11}$的值．

    查看答案和解析>>

    同步练习册答案