
【题目】如图,圆![]() 的直径为
的直径为![]() ,在圆
,在圆![]() 上位于直径
上位于直径![]() 的异侧有定点
的异侧有定点![]() 和动点
和动点![]() ,已知
,已知![]() ,点
,点![]() 在半圆弧
在半圆弧![]() 上运动(不与
上运动(不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 的延长线于
的延长线于![]() 点.
点.
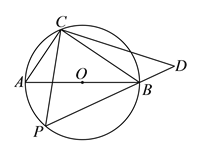
(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 运动到
运动到![]() 弧中点时,求
弧中点时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到什么位置时,
运动到什么位置时, ![]() 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积![]() .
.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )
)![]() ;(
;(![]() )
)![]() 为直径时最大,
为直径时最大, ![]() 最大值=
最大值=![]() .
.
【解析】试题分析:(1)由圆周角定理知∠CAB=∠CPD,而∠ACB=∠PCD=90°,即可判定△ABC∽△PCD,根据相似三角形的性质可得![]() ,即可得结论;(2)当点P运动到AB弧中点时,过点B作BE⊥PC于点E.由题意知∠PCB=45°,CE=BE,而又∠CAB=∠CPB,得tan∠CPB=tan∠CAB=
,即可得结论;(2)当点P运动到AB弧中点时,过点B作BE⊥PC于点E.由题意知∠PCB=45°,CE=BE,而又∠CAB=∠CPB,得tan∠CPB=tan∠CAB=![]() ,代入数值可求得PE的值,从而求得PC的值,由(1)知CD=
,代入数值可求得PE的值,从而求得PC的值,由(1)知CD=![]() PC,即可求得CD的长;(3)由题意知,S△PCD=
PC,即可求得CD的长;(3)由题意知,S△PCD=![]() PCCD.由(1)可知,CD=
PCCD.由(1)可知,CD=![]() PC即可得S△PCD=
PC即可得S△PCD=![]() PC2.故PC最大时,S△PCD取得最大值;而PC为直径时最大,即可求解.
PC2.故PC最大时,S△PCD取得最大值;而PC为直径时最大,即可求解.
试题解析:
(![]() )∵
)∵![]() 为直径,
为直径,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )当
)当![]() 运动到
运动到![]() 中点时,过
中点时,过![]() 作
作![]() 于点
于点![]() ,
,
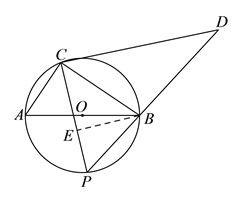
∵![]() 为直径,
为直径, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
∴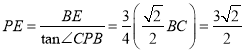 ,
,
从而![]() ,
,
由(![]() )得
)得![]() .
.
(![]() )当点
)当点![]() 在
在![]() 上运动时,
上运动时,
![]() ,由(
,由(![]() )得
)得![]() ,
,
∴![]() ,
,
故![]() 最大时,
最大时, ![]() 取得最大值.
取得最大值.
而![]() 为直径时最大,
为直径时最大,
∴![]() 最大值
最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】我们定义:两边平方和等于第三边平方的两倍的三角形叫做“奇异三角形”.
(1)根据“奇异三角形”的定义,请你判断命题:“等边三角形一定是奇异三角形” 是 命题.(填写“真命题、假命题”)
(2)在RtΔABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若RtΔABC是“奇异三角形”,则a:b:c= .
(3)如图,在四边形ACBD中,∠ACB=∠ADB=90°,AD=BD,若在四边形ACBD内存在点E使得AE=AD,CB=CE.
①求证:ΔACE是“奇异三角形”;
②当ΔACE是直角三角形时,且AC=![]() ,求线段AB 的长.
,求线段AB 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你画出一个以BC为底边的等腰ΔABC,使底边上的高AD=BC.
(1)求tanB和 sinB的值;
(2)在你所画的等腰ΔABC中设底边BC=5米,求腰上的高BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,还需再添加两个条件才能使
,还需再添加两个条件才能使![]() ,则不能添加的一组条件是( )
,则不能添加的一组条件是( )

A. AC=DE,∠C=∠EB. BD=AB,AC=DE
C. AB=DB,∠A=∠DD. ∠C=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
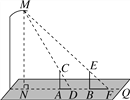
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com