
分析 (1)令y=0得到关于x的方程,可求得点A和点B的横坐标,令x=0求得对应的y值可得到点C的纵坐标;
(2)①由点A和点B的坐标可求得抛物线的对称轴为x=-m,则OD=m,然后证明△COD∽△EOC,依据相似三角形的性质可列出关于m的方程,从而可求得m的值;②证明△EQP∽△ECD、△EDF∽△PDH,然后依据相似三角形的性质得到$\frac{PQ}{DC}=\frac{PE}{DE}$、$\frac{PH}{EF}=\frac{DP}{DE}$,然后代入求解即可;
(3)首先依据题意画出符合题意得图形,接下来,再先求得点M的坐标,然后可求得MB的解析式,然后再求得∠AOT=60°,可得到TO的解析式,故此可求得K坐标和OK的长,然后证明OK=KM,设MN=a,TK=TO+OK=a+2$\sqrt{3}$,则△KTN的高h=TK•sin60°=$\frac{\sqrt{3}}{2}$a+3,NK=|2$\sqrt{3}$-a|,最后利用三角形的面积公式列方程求解即可.
解答 解:(1)令y=0得:0=-$\frac{1}{2m}$(x+3m)(x-m),解得:x=-3m或x=m,
∵点A在点B左侧,
∴A(-3m,0),B(m,0).
将x=0代入抛物线的解析式得:y=$\frac{3m}{2}$.
∴C(0,$\frac{3m}{2}$).
(2)∵A(-3m,0),B(m,0).
∴抛物线的对称轴为x=-m.
∴OD=m.
∵DE为圆的直径,
∴∠DCE=90°.
∵∠DCO+∠OCE=90°,∠DCO+∠CDO=90°,
∴∠OCE=∠CDO.
又∵∠DOC=∠COE,
∴△COD∽△EOC.
∴$\frac{CO}{OE}$=$\frac{OD}{OC}$即$\frac{\frac{3m}{2}}{\frac{9\sqrt{3}}{2}}$=$\frac{m}{\frac{3m}{2}}$,解得:m=2$\sqrt{3}$.
∴抛物线的解析式为y=-$\frac{\sqrt{3}}{12}$x2-x+3$\sqrt{3}$.
②如图1所示: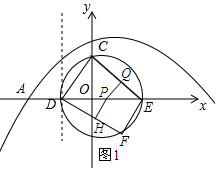
∵PQ⊥CE,
∴∠EQP=90°.
∴∠EQP=∠ECD.
又∵∠CED=∠QEP,
∴△EQP∽△ECD.
∴$\frac{PQ}{DC}=\frac{PE}{DE}$.
∵DE是圆的直径,
∴∠DFE=90°.
∵PH⊥DF,
∴∠DHP=90°.
∴∠DFE=∠DHP.
又∵∠PDH=∠EDF,
∴△EDF∽△PDH.
∴$\frac{PH}{EF}=\frac{DP}{DE}$.
∴$\frac{PQ}{DC}$+$\frac{PH}{EF}$=$\frac{PE+DP}{DE}$=$\frac{DE}{DE}$=1.
(3)如图3所示: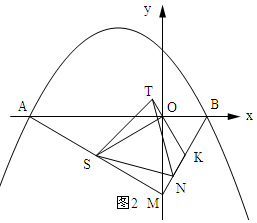
∵A(-3m,0),B(m,0),m=2$\sqrt{3}$,
∴A($-6\sqrt{3}$,0),B($2\sqrt{3}$,0).
∵∠OAM=30°,
∴OM=tan30°•OA=6$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=6,
∴M(0,-6).
设MB的解析式为y=kx+b,将点B和点M的坐标代入得:$\left\{\begin{array}{l}{b=-6}\\{2\sqrt{3}k+b=0}\end{array}\right.$,
解得:b=-6,k=$\sqrt{3}$.
∴BM的解析式为y=$\sqrt{3}$x-6.
∵S是线段AM的中点,∠AOM=90°,
∴OS=AS=$\frac{1}{2}$AM.
∴∠SAO=∠SOA=30°.
∵tan∠OMB=$\frac{OB}{OM}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠OMB=30°.
又∵∠OAM=30°,∠AOM=90°,
∴∠AMO=60°.
∴∠AMB=90°.
由旋转的性质可知:∠TOS=∠SMN=90°,TO=MN.
∴∠AOT=60°,
∴直线TK:y=-$\sqrt{3}$x.
将y=-$\sqrt{3}$x与y=$\sqrt{3}$x-6.联立,解得:K($\sqrt{3}$,-3).
依据两点间的距离可知:OK=$\sqrt{(\sqrt{3})^{2}+{3}^{2}}$=2$\sqrt{3}$.
∵∠B=60°,∠BOK=∠AOT=60°,
△OBK为等边三角形.
∴OB=KB.
又∵∠OMB=30°,∠BOM=90°,
∴MB=2OB.
∴MK=BK=OB=2$\sqrt{3}$.
设MN=a,TK=TO+OK=a+2$\sqrt{3}$,则△KTN的高h=TK•sin60°=$\frac{\sqrt{3}}{2}$a+3,NK=|2$\sqrt{3}$-a|,
∵S△KTN=$\frac{1}{12}$S△ABM=$\frac{1}{2}$•NK•h=2$\sqrt{3}$,
∴$\frac{1}{2}$×|2$\sqrt{3}$-a|×($\frac{\sqrt{3}}{2}a$+3)=2$\sqrt{3}$.
当2$\sqrt{3}$-a>0时,整理得:$\frac{\sqrt{3}}{4}$a2=$\sqrt{3}$,解得a=2或a=-2(舍去).
当2$\sqrt{3}$-a<0时,整理得:$\frac{\sqrt{3}}{4}$a2=5$\sqrt{3}$,解得:a=2$\sqrt{5}$或a=-$\sqrt{5}$(舍去).
综上所述,MN的长为2或$2\sqrt{5}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要二次函数的性质、圆周角定理、相似三角形的性质和判定、旋转的性质、等边三角形的性质和判定、待定系数法求一次函数的解析式,依据题意求得直线TK和BM的解析式是解答本题本题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:解答题
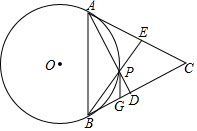 如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E.
如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
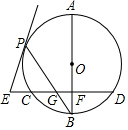 如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的反向延长线上,EP是⊙O的切线,
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的反向延长线上,EP是⊙O的切线,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com