
已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
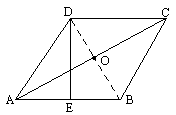
求:(1)∠ABC的度数;(2)对角线AC的长;(3)菱形ABCD的面积.
|
解:(1)连接BD, ∵四边形ABCD是菱形,∴AD=AB, 又∵E是AB的中点,且DE⊥AB,∴AD=DB, (只有等腰三角形才满足“三线合一”) ∴△ABD是等边三角形,∴△DBC也是等边三角形, ∴∠ABC= (2)∵四边形ABCD是菱形,∴AC与BD互相垂直平分, ∴OB= ∴OA= ∴AC=2OA= (3)菱形ABCD的面积S= (可以提炼出菱形的面积计算公式为:两对角线乘积的一半) 分析:我们没有菱形的运算公式,因此相应的运算必须借助三角形. |
|
注:本题考查菱形的性质,易错点是将平行四边形面积公式错用成三角形面积公式,解题关键是作辅助线,将菱形的问题转化成三角形问题来解决. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
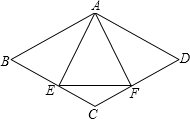 已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.
(2012•丰台区二模)已知:如图,菱形ABCD中,过AD的中点E作AC的垂线EF,交AB于点M,交CB的延长线于点F.如果FB的长是2,求菱形ABCD的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com