
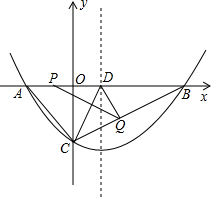
 ��֪��������y=$\frac{1}{16}$x2+bx+c��c��0����ͼ����x��ĸ���������ڵ�A����x����������ཻ�ڵ�B����y�ύ���C��8OC2=3OA•OB�ҡ�ABC�����Ϊ60��
��֪��������y=$\frac{1}{16}$x2+bx+c��c��0����ͼ����x��ĸ���������ڵ�A����x����������ཻ�ڵ�B����y�ύ���C��8OC2=3OA•OB�ҡ�ABC�����Ϊ60������ ��1������A��m��0����B��n��0����������mn=16c��OC=-c��OA•OB=-16c����8OC2=3OA•OB���г��������c���ٸ���$\left\{\begin{array}{l}{OA+OB=20}\\{OA•OB=96}\end{array}\right.$��OB��OA�����OA��OB���ɽ�����⣮
��2��������ڣ����ʱ��t��������߶�PQ��ֱ��CD��ֱƽ�֣����ɴ�ֱƽ���ߵ����ʼ����ɶ��������t����t�Ƿ���ڣ�
��3������ֱ��x=1���Ǵ��ڵ�M��ʹ��MPQΪ���������Σ���ʱҪ������������ۣ��ٵ�PQΪ������MPQ����ʱ����PΪ���㣻�ڵ�PQΪ������MPQ����ʱ����QΪ���㣻Ȼ���ٸ��ݵ��������ε����ʼ�ֱ�������εĹ��ɶ������M�����꣮
��� �⣻��1����A��m��0����B��n��0����
������mn=16c��
��OC=-c��OA•OB=-16c��
��8OC2=3OA•OB��
��8c2=3����-16c����
��c��0��
��c=-6��
��S��ABC=$\frac{1}{2}$AB•OC=60��
��AB=20��
��$\left\{\begin{array}{l}{OA+OB=20}\\{OA•OB=96}\end{array}\right.$
��OB��OA��
��OA=8��OB=12��
���A��-8��0����B��12��0����C��0��-6����
��0=$\frac{1}{16}$��64-8b-6��
��b=-$\frac{1}{4}$��
�������߽���ʽΪy=$\frac{1}{16}$x2-$\frac{1}{4}$x-6��
��2�����ڣ���ֱ��CD��ֱƽ��PQ��
��Rt��AOC��AC=$\sqrt{{6}^{2}+{8}^{2}}$=10=AD��
���D�ڶԳ����ϣ�����DQ����Ȼ��PDC=��QDC��
����֪��PDC=��ACD��
���QDC=��ACD��
��DQ��AC��
��DB=AB-AD=20-10=10��
��DQΪ��ABC����λ�ߣ�
��DQ=$\frac{1}{2}$AC=5��
��AP=AD-PD=AD-DQ=10-5=5��
��t=5��1=5���룩��
�����t=5���룩ʱ���߶�PQ��ֱ��CD��ֱƽ�֣�
��Rt��BOC��BC=$\sqrt{{6}^{2}+1{2}^{2}}$=6 $\sqrt{5}$��
��DQΪ��ABC����λ�ߣ�
��CQ=3 $\sqrt{5}$��
���Q���˶��ٶ�Ϊÿ�� $\frac{3\sqrt{5}}{5}$��λ���ȣ�
��3�����ڣ�����Q��QH��x����H����QH=3��PH=9
��Rt��PQH��PQ=$\sqrt{{9}^{2}+{3}^{2}}$=3 $\sqrt{10}$��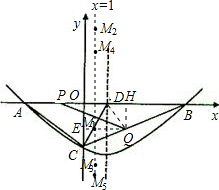
�ٵ�MP=MQ����MΪ���㣬
��ֱ��CD��ֱ�߷���Ϊ��y=kx+b��k��0����
��$\left\{\begin{array}{l}{b=-6}\\{2k+b=0}\end{array}\right.$��ã�$\left\{\begin{array}{l}{k=3}\\{b=-6}\end{array}\right.$��
��y=3x-6
��x=1ʱ��y=-3��
��M1��1��-3����
�ڵ�PQΪ������MPQ����ʱ����PΪ���㣮
��ֱ��x=1�ϴ��ڵ�M��1��y����
��OP=3����M�ĺ�����Ϊ1��������Ϊy�����ݹ��ɶ�����PM22=42+y2��
��PQ2=90��
��42+y2=90��
��y=��$\sqrt{74}$��
��M2��1��$\sqrt{74}$����M3��1��-$\sqrt{74}$����
�۵�PQΪ������MPQ����ʱ����QΪ���㣬
����Q��QE��y����E����ֱ��x=1��F����F��1��-3��
��ֱ��x=1���ڵ�M��1��y�����ɹ��ɶ����ã�
��y+3��2+52=90��y=-3��$\sqrt{65}$��
��M4��1��-3+$\sqrt{65}$ ����M5��1��-3-$\sqrt{65}$����
����������������������㣺
M1��1��-3����M2��1��$\sqrt{74}$����M3��1��-$\sqrt{74}$����M4��1��-3+$\sqrt{65}$����M5��1��-3-$\sqrt{65}$����
���� ������һ���ۺ��⣬�ѶȽϴ���Ҫ������κ��������ʣ��ô���ϵ���������Ľ���ʽ����������������ε����ʼ����ɶ�����ͬʱ����ѧ��̽�����������⣬�Դ�����Ҫ˼��ȫ�棬ѧ��������۵�˼�룬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ȷ��ʮ��λ����2����Ч���� | B�� | ��ȷ����λ����2����Ч���� | ||
| C�� | ��ȷ����λ����2����Ч���� | D�� | ��ȷ��ǧλ����4����Ч���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
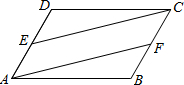 ��ͼ����֪E��F�ֱ��DZ�AD��BC���е㣬AD=BC��AD��BC����AF=CE����˵�����ɣ�
��ͼ����֪E��F�ֱ��DZ�AD��BC���е㣬AD=BC��AD��BC����AF=CE����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
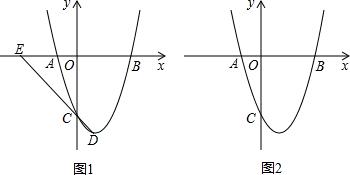
 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ���ҹ���x��һԪ���η���ax2+bx+c-m=9û��ʵ�����������н��ۣ�
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ���ҹ���x��һԪ���η���ax2+bx+c-m=9û��ʵ�����������н��ۣ�| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x+7=0 | B�� | x2+5x=-6 | C�� | x��x+5��=x3-1 | D�� | 3x2-$\frac{7}{x}$=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com