
问题“如图,已知点O在直线 上,以线段OD为一边画等腰三角形,且使另一顶点A在直线
上,以线段OD为一边画等腰三角形,且使另一顶点A在直线 上,则满足条件的A点有几个?”我们可以用圆规探究,按如图的方式,画图找到4个点:A1、A2、A3、A4,这种找点的过程中体现了( ▲ )的数学思想方法.
上,则满足条件的A点有几个?”我们可以用圆规探究,按如图的方式,画图找到4个点:A1、A2、A3、A4,这种找点的过程中体现了( ▲ )的数学思想方法.
| A.归纳与演绎 | B.分类讨论 | C.函数与方程 | D.转化与化归 |
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
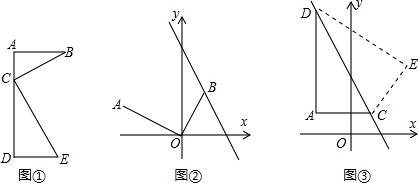
 29、实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.
29、实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.查看答案和解析>>
科目:初中数学 来源: 题型:
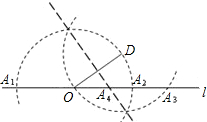
 6、问题:“如图,已知点O在直线l上,以线段OD为一边画等腰三角形,且使另一顶点A在直线l上,则满足条件的A点有几个?”.我们可以用圆规探究,按如图的方式,画图找到4个点:A1、A2、A3、A4.这种问题说明的方式体现了( )的数学思想方法.
6、问题:“如图,已知点O在直线l上,以线段OD为一边画等腰三角形,且使另一顶点A在直线l上,则满足条件的A点有几个?”.我们可以用圆规探究,按如图的方式,画图找到4个点:A1、A2、A3、A4.这种问题说明的方式体现了( )的数学思想方法.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
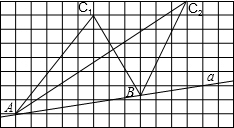 实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.
实践与操作:在课堂上,李老师和同学们探究了与三角形面积相关的问题.如图,已知点A、B同在直线a上,点C1、C2在直线a的同一侧.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.归纳与演绎 | B.分类讨论 | C.数形结合 | D.转化与化归 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com