
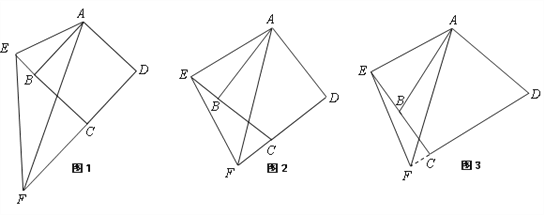
【题目】如图1,四边形ABCD,将顶点为A的角绕着顶点A顺时针旋转,若角的一条边与DC的延长线交于点F,角的另一条边与CB的延长线交于点E,连接EF.
●特例发现 若四边形ABCD为正方形,当∠EAF=45°时,则EF、DF、BE满足数量关系为 ;
●深入探究 如图2,如果在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,当∠EAF=![]() ∠BAD时,则EF、DF、BE满足数量关系为 ;
∠BAD时,则EF、DF、BE满足数量关系为 ;
如图3,如果四边形ABCD中,AB=AD,∠ABC与∠ADC互补,当∠EAF=![]() ∠BAD 时,EF与DF、BE之间的数量关系是否发生改变?请给出详细的证明过程;
∠BAD 时,EF与DF、BE之间的数量关系是否发生改变?请给出详细的证明过程;
●拓展应用 在(3)中,若BC=4,DC=7,CF=2,求△CEF的周长.
【答案】●特例发现, EF=DF-BE;●深入探究 ,EF=DF-BE;EF=DF-BE,证明见解析;●拓展应用△CEF的周长为15.
【解析】试题分析:“特例发现”与” “深入探究”解题思路一致,都是通过两步全等来实现;在DC上截取DG=BE,第一步,首先证△ADG≌△ABE,得AE=AG;第二步,证△AGF≌△AEF,得EF=GF,由此得到DF、EF、BE的数量关系.
根据前三问的结论知:EF=DF-BE,那么△CEF的周长可转化为:CE+EF+FC=CE+(DF-BE)+FC =BC+DC+2FC,从而得解.
试题解析:●特例发现 EF=DF-BE;
●深入探究 EF=DF-BE,
如图4,在DC上截取DG,使DG=BE,连接AG.
∵∠D+∠ABC=180°,∠ABC+∠ABE=180°,
∴∠ABE=∠D.
又∵AB=AD,DG=BE,
∴△ABE≌△ADG(SAS).
∴∠BAE=∠DAG,AE=AG.
又∵∠DAG+∠BAF=∠BAE+∠BAF=∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠BAD-(∠DAG+∠BAF)=![]() ∠BAD,
∠BAD,
∴∠GAF=∠EAF.
∵AE=AG (前面已证),AF=AF,
∴△AFE≌△AFG(SAS),
∴EF=GF.
∴EF=GF=DF-DG=DF-BE.

●拓展应用
△CEF的周长:CE+EF+FC=CE+(DF-BE)+FC
=(CE-BE)+DF+FC
=(CE-BE)+(DC+FC)+FC
=BC+DC+2FC
=4+7+2×2
=15.


科目:初中数学 来源: 题型:
【题目】观察下列算式:21=2、22=4、23=8、24=16、25=32、26=64、27=128、28=256….观察后,用你所发现的规律写出223的末位数字是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是位于我国东海钓鱼岛列岛的主岛,被誉为“深海中的翡翠”,面积约4400000平方米,数据4400000用科学记数法表示为( )
A.4.4×106
B.0.44×105
C.44×105
D.4.4×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某手机店1~4月份的统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )

A. 4月份三星手机销售额为65万元
B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(深圳中考)2016年深圳市“读书月”活动结束后,教育部门就某校初三学生在该活动期间阅读课外书籍的数量进行统计,将收集的数据绘制成如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题.

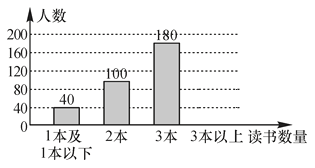
(1)x=_______,这次共抽取______名学生进行调查,并补全条形图;
(2)在学生读书数量扇形统计图中,3本以上所对扇形的圆心角度数是______;
(3)若全市在校初三年级学生有6.7万名,请你估计全市初三学生在本次“读书月”活动中读书数量在3本以上的学生约有________万名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com