
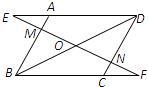
 21、已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
21、已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.

科目:初中数学 来源:数学教研室 题型:022
已知如图所示,在平行四边ABCD中,对角线相交于点O,已知AB=24cm,BC=18cm,△AOB的周长是54cm那么△AOD的周长是________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:022
已知如图所示,在平行四边ABCD中,对角线相交于点O,已知AB=24cm,BC=18cm,△AOB的周长是54cm那么△AOD的周长是________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
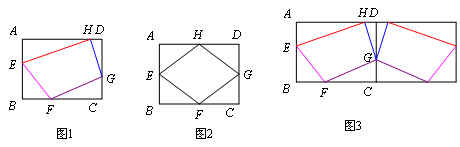
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m=________.
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.
①请在图1中补全小贝同学翻折后的图形;
②m的取值范围是____________.
【解析】本题主要考查对平行四边形的性质和判定,全等三角形的性质和判定等知识点的理解和掌握
查看答案和解析>>
科目:初中数学 来源:2012届北京市西城区九年级一模数学卷(解析版) 题型:解答题
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
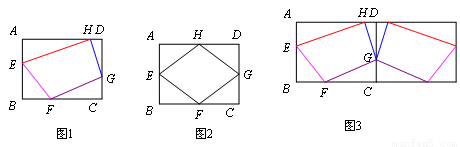
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m=________.
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.
①请在图1中补全小贝同学翻折后的图形;
②m的取值范围是____________.
【解析】本题主要考查对平行四边形的性质和判定,全等三角形的性质和判定等知识点的理解和掌握
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com