
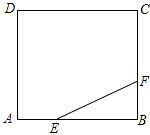
 (2013•舟山)如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程为
(2013•舟山)如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程为| 5 |
| 5 |
| 1 |
| 2 |
 解:根据已知中的点E,F的位置,可知入射角的正切值为
解:根据已知中的点E,F的位置,可知入射角的正切值为| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 5 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |


科目:初中数学 来源: 题型:
 (2013•舟山)如图,在平面直角坐标系xOy中,抛物线y=
(2013•舟山)如图,在平面直角坐标系xOy中,抛物线y=| 1 |
| 4 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•舟山)如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )
(2013•舟山)如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )查看答案和解析>>
科目:初中数学 来源: 题型:
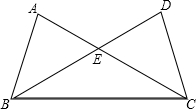 (2013•舟山)如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(2013•舟山)如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com