
【题目】我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,直接下列问题答案:
(1)|5﹣(﹣2)|的值为_____;
(2)若|x﹣3|=1,则x的值为_____;
(3)若|x﹣3|=|x+1|,则x的值为_____;
(4)若|x﹣3|+|x+1|=7,则x的值为_____.
![]()
【答案】7 2或4 1 ﹣2.5或4.5.
【解析】
(1)先求出![]() 的结果,再求出它的绝对值即可;
的结果,再求出它的绝对值即可;
(2)根据绝对值的性质得到![]() ,解方程即可求解;
,解方程即可求解;
(3)根据绝对值的意义,可知![]() 是数轴上表示数x的点与表示数3的点之间的距离,
是数轴上表示数x的点与表示数3的点之间的距离,![]() 是数轴上表示数x的点与表示数﹣1的点之间的距离,若
是数轴上表示数x的点与表示数﹣1的点之间的距离,若![]() ,则此点必在
,则此点必在![]() 与
与![]() 之间,故
之间,故![]() ,
,![]() ,由此可得到关于x的方程,求出x的值即可;
,由此可得到关于x的方程,求出x的值即可;
(4)由于![]() 及
及![]() 的符号不能确定,故应分
的符号不能确定,故应分![]() ,
,![]() ,
,![]() 三种情况解答.
三种情况解答.
解:(1)![]() 的值为7;
的值为7;
(2)∵![]() ,
,
∴![]() ,
,
解得x=2或4.
故x的值为2或4;
(3)根据绝对值的意义可知,此点必在![]() 与3之间,故
与3之间,故![]() ,
,![]() ,
,
∴原式可化为![]() ,
,
∴x=1.
故x的值为1;
(4)在数轴上3和![]() 的距离为4,则满足方程的x的对应点在
的距离为4,则满足方程的x的对应点在![]() 的左边或3的右边.
的左边或3的右边.
若x的对应点在![]() 的左边,则
的左边,则![]() ;
;
若x的对应点在3的右边,则![]() .
.
所以原方程的解是![]() 或x=4.5.
或x=4.5.
故x的值为![]() 或4.5.
或4.5.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE(顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接CE.
⑴ 如图1,若点D在BC边上(点D与B、C不重合),求∠BCE的度数.
⑵ 如图2,若点D在CB的延长线上,若DB=5,BC=7,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有200名学生.为了解该年级学生A课程的学习情况,从中随机抽取40名学生进行测试(测试成绩是百分制,且均为正整数), 并对数据(A课程测试成绩)进行整理、描述和分析.这组数据(A课程测试成绩)的平均分数是78.38. 下表是随机抽取的40名学生A课程测试成绩频数分布表
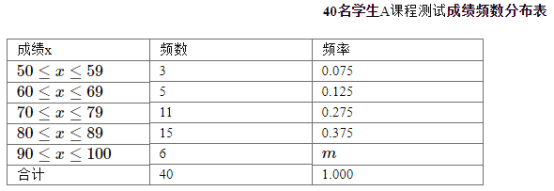
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)80分及以上的频数之和是21,79分及以下的频数之和是19,而平均分数(78.38)在80分以下. 由此可知,这次测验的成绩高于平均分的人数________(填“多”或“少”),低于平均分的人数________(填“多”或“少”),成绩属偏________(填“高”或“低”)分布;
(3)假设该年级学生都参加此次测试,估计这次A课程测试成绩90分及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
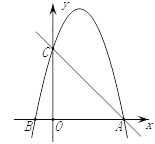
【题目】如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.
(1)求抛物线的函数表达式;
(2)在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.
(3)在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月25日至27日,第二届“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议。我国准备将![]() 地的茶叶1000吨和
地的茶叶1000吨和![]() 地的茶叶500吨销往“一带一路”沿线的
地的茶叶500吨销往“一带一路”沿线的![]() 地和
地和![]() 地,
地,![]() 地和
地和![]() 地对茶叶需求分别为900吨和600吨,已知从
地对茶叶需求分别为900吨和600吨,已知从![]() 、
、![]() 两地运茶叶到
两地运茶叶到![]() 、
、![]() 两地的运费(元/吨)如下表所示,设
两地的运费(元/吨)如下表所示,设![]() 地运到
地运到![]() 地的茶叶为
地的茶叶为![]() 吨,
吨,
|
| |
| 35 | 40 |
| 30 | 45 |
(1)用含![]() 的代数式填空:
的代数式填空:![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________,
地的茶叶吨数为___________,![]() 地运往
地运往![]() 地的茶叶吨数为___________.
地的茶叶吨数为___________.
(2)用含![]() (吨)的代数式表示总运费
(吨)的代数式表示总运费![]() (元),并直接写出自变量
(元),并直接写出自变量![]() 的取值范围;
的取值范围;
(3)求最低总运费,并说明总运费最低时的运送方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料解决问题
两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” B.345和513互为“调和数
C.2018和8120互为“调和数” D.两位数![]() 和
和![]() 互为“调和数”
互为“调和数”
(2)若A、B是两个不等的两位数,A=![]() ,B=
,B=![]() ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com