
分析 (1)根据分式的加减乘除混合运算顺序进行计算,注意进行因式分解和约分.
(2)根据分式的加减乘除混合运算顺序进行计算,注意进行因式分解和约分.
(3)根据分式的加减乘除混合运算顺序进行计算,注意进行因式分解和约分.
(4)根据分式的加减法法则进行计算,注意通分.
解答 解:(1)(1-$\frac{1}{1-x}$)÷$\frac{x}{x-1}$.
=$\frac{x-1+1}{x-1}$×$\frac{x-1}{x}$
=1
(2)$\frac{b}{a-b}$+$\frac{{b}^{3}}{{a}^{3}-2{a}^{2}b+a{b}^{2}}$÷$\frac{ab+{b}^{2}}{{b}^{2}-{a}^{2}}$
=$\frac{b}{a-b}$+$\frac{{b}^{3}}{a(a-b)^{2}}$×$\frac{-(a+b)(a-b)}{b(a+b)}$
=$\frac{b}{a-b}$-$\frac{{b}^{2}}{a(a-b)}$
=$\frac{ab-{b}^{2}}{a(a-b)}$
=$\frac{b}{a}$
(3)($\frac{a-b}{a+b}$-$\frac{a+b}{a-b}$)÷(1-$\frac{{a}^{2}+{b}^{2}}{{a}^{2}-2ab+{b}^{2}}$)
=$\frac{(a-b)^{2}-(a+b)^{2}}{(a+b)(a-b)}$×$\frac{{a}^{2}-2ab+{b}^{2}-{a}^{2}-{b}^{2}}{(a-b)^{2}}$
=$\frac{-4ab}{(a+b)(a-b)}$×$\frac{(a-b)^{2}}{-2ab}$
=$\frac{2a-2b}{a+b}$
(4)$\frac{{a}^{2}}{a-1}$-a-1
=$\frac{{a}^{2}-({a}^{2}-1)}{a-1}$
=$\frac{1}{a-1}$
点评 本题考查了分式的混合运算、分式的约分、通分以及因式分解;熟练掌握分式的混合运算顺序和因式分解是解决问题的关键..


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:填空题
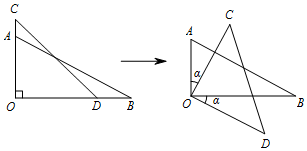 将两块直角三角尺的直角顶点重合为如图所示的位置,△COD为等腰直角三角形,当△COD绕点O顺时针旋转α度(0<α<90),∠COB:∠BOD=3:2时,则∠BOC=54°.
将两块直角三角尺的直角顶点重合为如图所示的位置,△COD为等腰直角三角形,当△COD绕点O顺时针旋转α度(0<α<90),∠COB:∠BOD=3:2时,则∠BOC=54°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
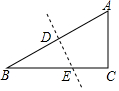 如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=4cm,现将△ABC沿直线DE翻折,使点A和点B重合,则折痕DE长为$\sqrt{5}$cm.
如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=4cm,现将△ABC沿直线DE翻折,使点A和点B重合,则折痕DE长为$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
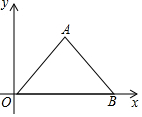 如图,在平面直角坐标系中,△AOB为等腰直角三角形A(4,4),点C从O出发,以2个单位/秒的速度沿x轴正方向运动.
如图,在平面直角坐标系中,△AOB为等腰直角三角形A(4,4),点C从O出发,以2个单位/秒的速度沿x轴正方向运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
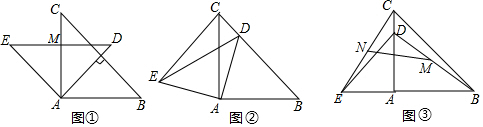
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com