
【题目】如图,在![]() 中,∠C=90°,O是斜边AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与BC交于点F,与AC相切于点D,连接DF、BD,且BD平分∠ODF.
中,∠C=90°,O是斜边AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与BC交于点F,与AC相切于点D,连接DF、BD,且BD平分∠ODF.
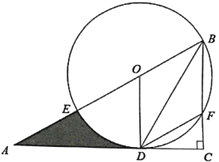
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() ).
).
【答案】(1)证明见解析;(2)S阴影=![]() .
.
【解析】
(1)由切线的性质可得∠ODA=90°,可证明OD//BC,根据等腰三角形的性质可得∠ODB=∠OBD,由角平分线的定义可得∠ODB=∠BDF,可证明较OBD=∠BDF,可证明OB//DF,可得四边形ODFB是平行四边形,根据OB=OD可证明四边形ODFB是菱形;
(2)如图,连接OF,根据菱形的性质可证明△OBF是等边三角形,可得∠FBC=60°,可得∠A=30°,根据平行线的性质可得∠FOD=60°,利用∠FOD的正切函数可求出OD的长,根据S阴影=S△ADO-S扇形OED即可求出阴影部分面积.
(1)∵⊙O与AC相切于点D,
∴OD⊥AC,∠ODA=90°,
∵∠C=90°,
∴OD//BC,
∵OB=OD,
∴∠ODB=∠OBD,
∵BD平分∠ODF,
∴∠ODB=∠BDF,
∴∠OBD=∠BDF,
∴OB//DF,
∴四边形ODFB是平行四边形,
∵OD=OB,
∴四边形ODBF是菱形.
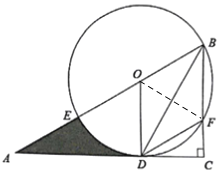
(2)如图,连接OF,
∵四边形ODFB是菱形,
∴OB=BF,
∵OB=OF,
∴△OBF是等边三角形,
∴∠ABC=60°,
∵OD//BC,
∴∠FOD=∠ABC=60°,
∵AD=3,
∴OD=![]() =
=![]() ,
,
∴S阴影=S△ADO-S扇形OED=![]() AD·OD-
AD·OD-![]() =
=![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】京九铁路“南昌到赣州”段是连接省会城市与江西南大门城市的重要通道.一列快车从南昌开往赣州,列慢车从赣州开往南昌,两车同时出发,设慢车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.
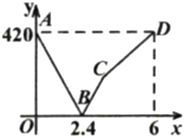
(1)慢车的速度为________![]() ,快车的速度为________
,快车的速度为________![]() ;
;
(2)当快车到达终点赣州后,求![]() 与
与![]() 之间的函数关系.
之间的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过⊙T外一点P引它的两条切线,切点分别为M,N,若![]() ,则称P为⊙T的环绕点.
,则称P为⊙T的环绕点.
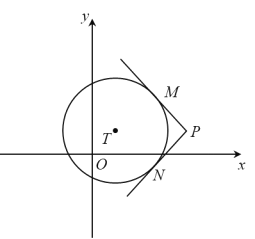
(1)当⊙O半径为1时,
①在![]() 中,⊙O的环绕点是___________;
中,⊙O的环绕点是___________;
②直线y=2x+b与x轴交于点A,y轴交于点B,若线段AB上存在⊙O的环绕点,求b的取值范围;
(2)⊙T的半径为1,圆心为(0,t),以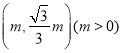 为圆心,
为圆心,![]() 为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.
为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
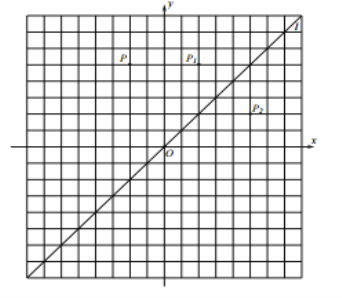
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 为一、三象限角平分线,点
为一、三象限角平分线,点![]() 关于
关于![]() 轴的对称点称为
轴的对称点称为![]() 的一次反射点,记作
的一次反射点,记作![]() ;
;![]() 关于直线
关于直线![]() 的对称点称为点
的对称点称为点![]() 的二次反射点,记作
的二次反射点,记作![]() .
.
例如,点![]() 的一次反射点为
的一次反射点为![]() ,二次反射点为
,二次反射点为![]() .
.
根据定义,回答下列问题:
(1)点![]() 的一次反射点为__________,二次反射点为____________;
的一次反射点为__________,二次反射点为____________;
(2)当点![]() 在第一象限时,点
在第一象限时,点![]() ,
,![]() ,
,![]() 中可以是点
中可以是点![]() 的二次反射点的是___________;
的二次反射点的是___________;
(3)若点![]() 在第二象限,点
在第二象限,点![]() ,
,![]() 分别是点
分别是点![]() 的一次、二次反射点,
的一次、二次反射点,![]() 为等边三角形,求射线
为等边三角形,求射线![]() 与
与![]() 轴所夹锐角的度数.
轴所夹锐角的度数.
(4)若点![]() 在
在![]() 轴左侧,点
轴左侧,点![]() ,
,![]() 分别是点
分别是点![]() 的一次、二次反射点,
的一次、二次反射点,![]() 是等腰直角三角形,请直接写出点
是等腰直角三角形,请直接写出点![]() 在平面直角坐标系
在平面直角坐标系![]() 中的位置.
中的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
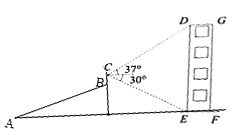
【题目】某同学利用数学知识测量建筑物DEFG的高度.他从点![]() 出发沿着坡度为
出发沿着坡度为![]() 的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端
的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端![]() 的仰角为37°,建筑物底端
的仰角为37°,建筑物底端![]() 的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到
的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() )( )
)( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
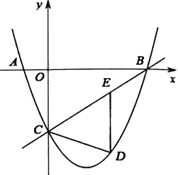
【题目】如图,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 连接
连接![]() ,已知
,已知![]()
![]() ,且
,且![]() ,
,
(1)求抛物线的解析式;
(2)若点![]() 为直线
为直线![]() 下方抛物线上一动点,过点
下方抛物线上一动点,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() 点,连接
点,连接![]()
①若![]() ,求此时点
,求此时点![]() 的坐标;
的坐标;
②若点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在
恰好落在![]() 轴上,求此时点
轴上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
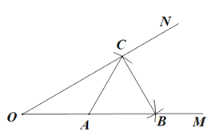
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出六个函数解析式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
小明根据学习二次函数的经验,分析了上面这些函数解析式的特点,研究了它们的图象和性质。下面是小明的分析和研究过程,请补充完整:
(1)观察上面这些函数解析式,它们都具有共同的特点,可以表示为形如![]() _______,其中x为自变量;
_______,其中x为自变量;
(2)如图,在平面直角坐标系![]() 中,画出了函数
中,画出了函数![]() 的部分图象,用描点法将这个函数的图象补充完整;
的部分图象,用描点法将这个函数的图象补充完整;
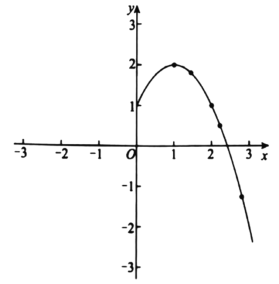
(3)对于上面这些函数,下列四个结论:
①函数图象关于y轴对称
②有些函数既有最大值,同时也有最小值
③存在某个函数,当![]() (m为正数)时,y随x的增大而增大,当
(m为正数)时,y随x的增大而增大,当![]() 时,y随x的增大而减小
时,y随x的增大而减小
④函数图象与x轴公共点的个数只可能是0个或2个或4个
所有正确结论的序号是________;
(4)结合函数图象,解决问题:若关于x的方程![]() 有一个实数根为3,则该方程其它的实数根为_______.
有一个实数根为3,则该方程其它的实数根为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
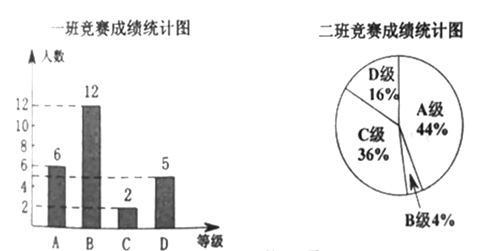
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com