
ЁОЬтФПЁПЯжга![]() ИіжЪЕиЁЂДѓаЁЭъШЋЯрЭЌЕФаЁЧђЩЯЗжБ№БъгаЪ§зж
ИіжЪЕиЁЂДѓаЁЭъШЋЯрЭЌЕФаЁЧђЩЯЗжБ№БъгаЪ§зж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЯШНЋБъгаЪ§зж
ЃЎЯШНЋБъгаЪ§зж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФаЁЧђЗХдкЕквЛИіВЛЭИУїЕФКазгРяЃЌдйНЋЦфграЁЧђЗХдкЕкЖўИіВЛЭИУїЕФКазгРяЃЎЯжДгЕквЛИіКазгРяЫцЛњШЁГівЛИіаЁЧђЃЌдйДгЕкЖўИіКазгРяЫцЛњШЁГівЛИіаЁЧђЃЎСНДЮЗжБ№гУxЁЂyРДБэЪОЃЎ
ЕФаЁЧђЗХдкЕквЛИіВЛЭИУїЕФКазгРяЃЌдйНЋЦфграЁЧђЗХдкЕкЖўИіВЛЭИУїЕФКазгРяЃЎЯжДгЕквЛИіКазгРяЫцЛњШЁГівЛИіаЁЧђЃЌдйДгЕкЖўИіКазгРяЫцЛњШЁГівЛИіаЁЧђЃЎСНДЮЗжБ№гУxЁЂyРДБэЪОЃЎ
ЃЈ1ЃЉЧыРћгУСаБэЛђЛЪїзДЭМЕФЗНЗЈжаЕФвЛжжЗНЗЈЃЌЧѓ(xЃЌy)ЫљгаПЩФмГіЯжЕФНсЙћзмЪ§ЃЛ
ЃЈ2ЃЉЧѓШЁГіЕФСНИіаЁЧђЩЯЕФЪ§зжжЎКЭЕШгк![]() ЕФИХТЪЃЎ
ЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЙВга6жжЕШПЩФмЕФНсЙћЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌСаГіБэИёМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉгЩБэИёПЩЕУЃЈxЃЌy)Ъ§зжжЎКЭЮЊ0ЕФНсЙћгаЃЈ1ЃЌ-1ЃЉЃЌЃЈ-2ЃЌ2ЃЉСНжжЃЌШЛКѓРћгУИХТЪЙЋЪНЧѓИХТЪМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЯТБэЃК
y x | -2 | 1 | 3 |
-1 | ЃЈ-2ЃЌ-1ЃЉ | ЃЈ1ЃЌ-1ЃЉ | ЃЈ3ЃЌ-1ЃЉ |
2 | ЃЈ-2ЃЌ2ЃЉ | ЃЈ1ЃЌ2ЃЉ | ЃЈ3ЃЌ2) |
ЙВга6жжЕШПЩФмЕФНсЙћЃЛ
ЃЈ2ЃЉЃЈxЃЌy)Ъ§зжжЎКЭЮЊ0ЕФНсЙћгаЃЈ1ЃЌ-1ЃЉЃЌЃЈ-2ЃЌ2ЃЉСНжж
![]() ШЁГіЕФСНИіаЁЧђЩЯЕФЪ§зжжЎКЭЕШгк
ШЁГіЕФСНИіаЁЧђЩЯЕФЪ§зжжЎКЭЕШгк![]() ЕФИХТЪЮЊ
ЕФИХТЪЮЊ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃЮЊСЫНтШЋаЃ2000УћбЇЩњЕНаЃЩЯбЇЕФЗНЪНЃЌдкШЋаЃЫцЛњГщШЁСЫШєИЩУћбЇЩњНјааЮЪОэЕїВщЃЎЮЪОэИјГіСЫЮхжжЩЯбЇЗНЪНЙЉбЇЩњбЁдёЃЌУПШЫжЛФмбЁвЛЯюЃЌЧвВЛФмВЛбЁЃЌНЋЕїВщЕУЕНЕФНсЙћЛцжЦГЩШчЭМЫљЪОЕФЭГМЦЭМКЭЦЕЪ§БэЃЈОљВЛЭъећЃЉЃЎ
ЕНаЃЗНЪН | ЦЕЪ§ | ЦЕТЪ |
здааГЕ | 24 | 0.3 |
ВНаа | ||
ЙЋНЛГЕ | 0.325 | |
ЫНМвГЕ | 10 | |
ЦфЫћ | 4 |
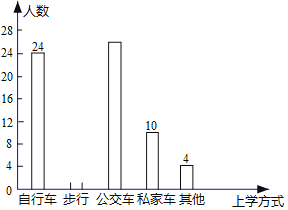
гЩЭМБэжаИјГіЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЮЪЃКдкетДЮЕїВщжаЃЌвЛЙВГщШЁСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЎ
ЃЈ3ЃЉЙРМЦШЋаЃЫљгабЇЩњжагаЖрЩйШЫВНааЩЯбЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњККДњЪ§бЇМведЫЌЮЊСЫжЄУїЙДЙЩЖЈРэЃЌДДжЦСЫвЛИБЁАЯвЭМЁБЃЌКѓШЫГЦЦфЮЊЁАедЫЌЯвЭМЁБЃЈШчЭМ1ЃЉЃЎЭМ2гЩЯвЭМБфЛЏЕУЕНЃЌЫќгЩЫФИіШЋЕШЕФжБНЧШ§НЧаЮЦДНгЖјГЩЃЎЕуEЃЌFЃЌGЃЌHЗжБ№ЪЧAFЃЌBGЃЌCHЃЌDEЕФжаЕуЃЌЕуMЃЌNЃЌPЃЌQЗжБ№ЪЧHEЃЌEFЃЌFGЃЌGHЩЯЕФжаЕуЃЌЧвЫФБпаЮMNPQЪЧе§ЗНаЮЃЌвбжЊе§ЗНаЮABCDЕФУцЛ§ЮЊ20ЃЌдђе§ЗНаЮMNPQЕФУцЛ§ЪЧЃЈ ЃЉЃЎ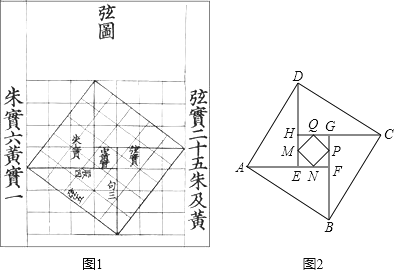
A.2B.1C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩЬЕъЙКНјвЛХњЕЅМлЮЊ20дЊЕФTаєЃЌОЪдЯњЗЂЯжЃЌУПЬьЯњЪлМўЪ§yЃЈМўЃЉгыЯњЪлМлИёxЃЈдЊ/МўЃЉТњзуШчЭМЕФвЛДЮКЏЪ§ЙиЯЕЃЎ
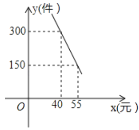
ЃЈ1ЃЉЧѓyгыxжЎМфКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіxШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉдкВЛПМТЧЛ§бЙЕШвђЫиЧщПіЯТЃЌЯњЪлМлИёЖЈЮЊЖрЩйЪБЃЌУПЬьЛёЕУРћШѓWзюДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉСЌНг![]() ЃЌгУЕШЪНБэЪОЯпЖЮ
ЃЌгУЕШЪНБэЪОЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ(гУКЌ
ЕФГЄ(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛ
ЕФДњЪ§ЪНБэЪО)ЃЛ
ЃЈ3ЃЉбгГЄЯпЖЮ![]() ЕН
ЕН![]() ЃЌбгГЄЯпЖЮ
ЃЌбгГЄЯпЖЮ![]() ЕН
ЕН![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЂкШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAD=![]() ABЃЌЁЯBADЕФЦНЗжЯпНЛBCгкЕуEЃЌDHЁЭAEгкЕуHЃЌСЌНгBHВЂбгГЄНЛCDгкЕуFЃЌСЌНгDEНЛBFгкЕуOЃЌЯТСаНсТлЃКЂйЁЯAED=ЁЯCEDЃЛЂкOE=ODЃЛЂлBH=HFЃЛЂмBCЉCF=2HEЃЛЂнAB=HFЃЌЦфжае§ШЗЕФгаЃЈ ЃЉ
ABЃЌЁЯBADЕФЦНЗжЯпНЛBCгкЕуEЃЌDHЁЭAEгкЕуHЃЌСЌНгBHВЂбгГЄНЛCDгкЕуFЃЌСЌНгDEНЛBFгкЕуOЃЌЯТСаНсТлЃКЂйЁЯAED=ЁЯCEDЃЛЂкOE=ODЃЛЂлBH=HFЃЛЂмBCЉCF=2HEЃЛЂнAB=HFЃЌЦфжае§ШЗЕФгаЃЈ ЃЉ

A. 2Иі B. 3Иі C. 4Иі D. 5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§бЇПЮЩЯЃЌЭЌбЇУЧвбОЬНОПЙ§ЁАОЙ§вбжЊжБЯпЭтвЛЕузїетЬѕжБЯпЕФДЙЯпЁБЕФГпЙцзїЭМЃК
вбжЊЃКжБЯпlКЭlЭтвЛЕуPЃЎ

ЧѓзїЃКжБЯпlЕФДЙЯпЃЌЪЙЫќОЙ§ЕуPЃЎ
зіЗЈЃКШчЭМЃКЃЈ1ЃЉдкжБЯпlЩЯШЮШЁСНЕуAЁЂBЃЛ
ЃЈ2ЃЉЗжБ№вдЕуAЁЂBЮЊдВаФЃЌ![]() ЁЂ
ЁЂ![]() ГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуQЃЛ
ГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуQЃЛ
ЃЈ3ЃЉзїжБЯп![]() ЃЎ
ЃЎ
ВЮПМвдЩЯВФСЯзїЭМЕФЗНЗЈЃЌНтОівдЯТЮЪЬтЃК
ЃЈ1ЃЉвдЩЯВФСЯзїЭМЕФвРОнЪЧ__________________ЃЎ
ЃЈ2ЃЉвбжЊЃКжБЯпlКЭlЭтвЛЕуPЃЎ
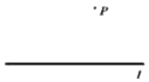
ЧѓзїЃК![]() ЃЌЪЙЫќгыжБЯпlЯрЧагкЕуCЃЈГпЙцзїЭМЃЌВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЎ
ЃЌЪЙЫќгыжБЯпlЯрЧагкЕуCЃЈГпЙцзїЭМЃЌВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЎ
ЃЈ3ЃЉЭъГЩЯТУцЕФжЄУїЃЎ
жЄУїЃКЁп![]() _____________ЃЌЧв
_____________ЃЌЧв![]() ___________ЃЎ
___________ЃЎ
ЁржБЯпlЪЧPЕФЧаЯпЃЈ_____________________ЃЉЃЈЬюЭЦРэЕФвРОнЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНax2+bx+cОЙ§ЕуAЃЌЕуBЃЌгыyжсИКАыжсНЛгкЕуCЃЌЧвOCЃНOBЃЌЦфжаBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЌЖдГЦжсlЮЊжБЯпxЃН![]() ЃЌDЮЊХзЮяЯпЖЅЕуЃЎ
ЃЌDЮЊХзЮяЯпЖЅЕуЃЎ
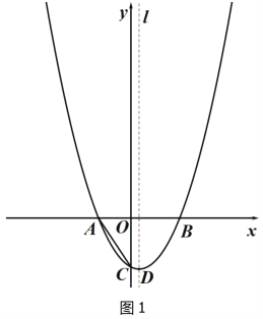
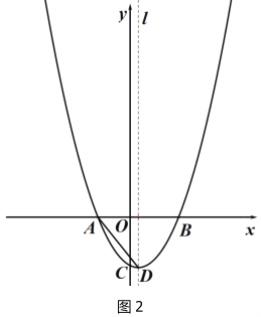
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉPЮЊХзЮяЯпЩЯвЛЕуЃЈВЛгыCжиКЯЃЉЃЌКсзјБъЮЊmЃЌСЌНгAPЃЌШєЁЯPABЃНЁЯCABЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌAPНЛlгкЕуQЃЌСЌНгADЃЌЕуNЮЊЯпЖЮQDЩЯвЛЖЏЕуЃЈВЛгыQЁЂDжиКЯЃЉЃЌЧвЕуNЕФзнзјБъЮЊnЃЎЙ§ЕуNзїжБЯпгыЯпЖЮDAЯрНЛгкЕуMЃЌШєЖдгкУПвЛИіШЗЖЈЕФnЕФжЕЃЌгаЧвжЛгавЛИіЁїDMNгыЁїDAQЯрЫЦЃЌЧыжБНгаДГіnЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎвбжЊЕу
ЃЎвбжЊЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉжБЯп![]() гыХзЮяЯпНЛгк
гыХзЮяЯпНЛгк![]() СНЕуЃЌХзЮяЯпЕФЖдГЦжсЮЊжБЯп
СНЕуЃЌХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]()
ЂйЧѓ![]() ЃЌ
ЃЌ![]() ЫљТњзуЕФЪ§СПЙиЯЕЪНЃЛ
ЫљТњзуЕФЪ§СПЙиЯЕЪНЃЛ
ЂкЕБOP=OAЪБЃЌЧѓЯпЖЮ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com