
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动,连接AD、AE,设运动时间为t秒. 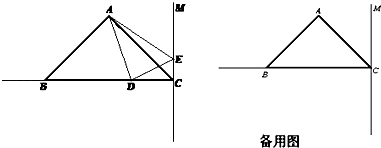
(1)求AB的长;
(2)当t为多少时,△ABD的面积为6cm2?
(3)当t为多少时,△ABD≌△ACE,并简要说明理由.(可在备用图中画出具体图形)
【答案】
(1)解:∵在△ABC中,AB=AC,∠BAC=90°,
∴2AB2=BC2,
∴AB= ![]() =3
=3 ![]() cm;
cm;
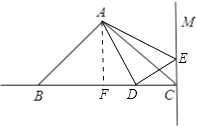
(2)解:过A作AF⊥BC交BC于点F,则AF= ![]() BC=3cm,
BC=3cm,
∵S△ABD=6cm2,
∴AF×BD=12,
∴BD=4cm.
若D在B点右侧,则CD=2cm,t=1s;
若D在B点左侧,则CD=10cm,t=5s.
(3)解:动点E从点C沿射线CM方向运动2秒或当动点E从点C沿射线CM的反向延长线方向运动6秒时,△ABD≌△ACE.
理由如下:(说理过程简要说明即可)
①当E在射线CM上时,D必在CB上,则需BD=CE.
∵CE=t,BD=6﹣2t∴t=6﹣2t∴t=2
证明:∵AB=AC,∠B=∠ACE=45°,BD=CE,
∴△ABD≌△ACE.
②当E在CM的反向延长线上时,D必在CB延长线上,则需BD=CE.
∵CE=t,BD=2t﹣6∴t=2t﹣6∴t=6
证明:∵AB=AC,∠ABD=∠ACE=135°,BD=CE
∴△ABD≌△ACE.
【解析】(1)运用勾股定理直接求出;(2)首先求出△ABD中BD边上的高,然后根据面积公式列出方程,求出BD的值,分两种情况分别求出t的值;(3)假设△ABD≌△ACE,根据全等三角形的对应边相等得出BD=CE,分别用含t的代数式表示CE和BD,得到关于t的方程,从而求出t的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④ ![]() 其中正确的有( )
其中正确的有( )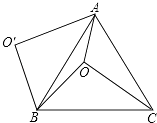
A.①②
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n满足等式(m﹣8)2+2|n﹣m+5|=0.
(1)求m,n的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=nPB,点Q为PB的中点,求线段AQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com