
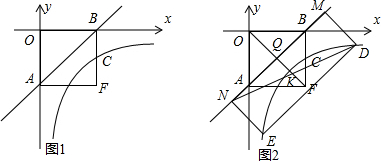
���� ��1������ֱ��y=x-2��x�ᡢy�ύ�ڵ�B��A���������A��B�����꣬�ɴ˼��ɵó���F�����꣬���ɵ�CΪBF���е㣬�����C�����꣬��ϵ�C���������÷���������ͼ���ϵ�����������������˫���ߵĽ���ʽ��
��2��������ڣ������ֱ�ߵĽ���ʽΪy=kx+b��k��0�����ɵ�F�ڸ�ֱ���Ͽ���k��ʾ��bֵ����ֱ�߽���ʽ����˫���߽���ʽ���ҳ�����x��һԪ���η��̣���������ΪP1��x1��y1����P2��x2��y2�������ݸ���ϵ���Ĺ�ϵ���ҳ�x1+x2=$\frac{2��k+1��}{k}$��x1•x2=$\frac{2}{k}$���ɴ˼������������ľ��빫ʽ���P1 P2���������2���ɵó�����k��һԪ���η��̣����ɸ����б�ʽ�ó��÷����⣬�Ӷ��ó����費���ˣ��ɴ˼��ɵó����ۣ�
��3����E��EG��x�ύֱ��y=x-2��G����E������Ϊ��x��y����G������Ϊ��x0��y�����������ľ��빫ʽ����߶�EF��EG���Ӷ��ó���EGNΪ����ֱ�������Σ��ٸ���ƽ���ߵ������ҳ����߶μ�ı�����ϵ���Ӷ��ó�FK=QK������ý⣮
��� �⣺��1����ֱ��y=x-2��x�ᡢy�ύ�ڵ�B��A��
���B��2��0������A��0��-2����
�߹�A��B����քe��y�ᡢx��Ĵ��߽��ڵ�F��
���F��2��-2����
�ߵ�CΪBF���е㣬
���C��2��-1����
��˫����y=$\frac{m}{x}$ ��x��0��������C��
��m=2����-1��=-2��
��˫���ߵĽ���ʽΪy=-$\frac{2}{x}$��
��2��������ڣ�ֱ��l��y=kx+b��k��0����
�ߵ�F��2��-2����ֱ��l�ϣ�
��-2=2k+b��b=-2k-2��
��y=kx-2k-2��
��y=kx-2k-2����y=-$\frac{2}{x}$�У��ã�kx-2k-2=-$\frac{2}{x}$��
�����ã�kx2-2��k+1��x+2=0��
��������ΪP1��x1��y1����P2��x2��y2�������ɸ���ϵ���Ĺ�ϵ�ã�
x1+x2=$\frac{2��k+1��}{k}$��x1•x2=$\frac{2}{k}$��
��P1 P2=$\sqrt{��{x}_{2}-{x}_{1}��^{2}+��{y}_{2}-{y}_{1}��^{2}}$=$\sqrt{��1+{k}^{2}����{x}_{2}-{x}_{1}��^{2}}$=$\sqrt{��1+{k}^{2}��[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{��1+{k}^{2}��[\frac{4��k+1��^{2}}{{k}^{2}}-\frac{8}{k}]}$=$\sqrt{\frac{4��1+{k}^{2}��^{2}}{{k}^{2}}}$=$\frac{2��1+{k}^{2}��}{|k|}$��
��P1 P2=2��k��0����$\frac{2��1+{k}^{2}��}{|k|}$=2��
��k2-k+1=0��
�ߡ�=-3��0��
��˷�����ʵ���������費������
�ʲ�����ֱ��l��˫����������ľ�����2��
��3��֤������E��EG��x�ύֱ��y=x-2��G�����EGNΪ����ֱ�������Σ���ͼ��ʾ��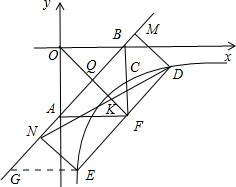
��E��������x��y����G��������x0��y����
��G��x0��y����ֱ��ֱ��y=x-2�ϣ�
��y=x0-2��
�֡ߵ�E��x��y����˫����C��y=-$\frac{2}{x}$��x��0���ϣ�
��-$\frac{2}{x}$=x0-2������x0=-$\frac{2}{x}$+2��
����EG=x-x0=x+$\frac{2}{x}$-2��
�֡�EF=$\sqrt{��x-2��^{2}+��y+2��^{2}}$=$\sqrt{��x-2��^{2}+��-\frac{2}{x}+2��^{2}}$=$\sqrt{��x+\frac{2}{x}��^{2}-4��x+\frac{2}{x}��+4}$=$\sqrt{��x+\frac{2}{x}-2��^{2}}$=|x+$\frac{2}{x}$-2|��
��x+y��2$\sqrt{xy}$��x��0��y��0����
��x+$\frac{2}{x}$��2$\sqrt{x•\frac{2}{x}}$=2$\sqrt{2}$��x��0�����ҽ���x=$\frac{2}{x}$ʱ������ʽȡ�Ⱥţ���
��EF=|x+$\frac{2}{x}$-2|=x+$\frac{2}{x}$-2����EG=EF��
���EGNΪ����ֱ�������Σ�
��ED=$\sqrt{2}$EN��
ͬ���ɵã�DF=$\sqrt{2}$DM��
��EN=a��DM=b��
��EF=$\sqrt{2}$a��DF=$\sqrt{2}$b��
��EN��AB��OF��AB��
��FQ��EN��
��$\frac{FK}{EN}=\frac{DF}{DE}$��
��FK=$\frac{DF•EN}{DE}$=$\frac{\sqrt{2}ab}{\sqrt{2}a+\sqrt{2}b}$=$\frac{ab}{a+b}$��
ͬ���ɵã�FK��DM��
��$\frac{QK}{DM}=\frac{NQ}{NM}=\frac{EF}{DE}$��
��QK=$\frac{EF•DM}{DE}$=$\frac{\sqrt{2}ab}{\sqrt{2}a+\sqrt{2}b}$=$\frac{ab}{a+b}$��
��FK=QK��
��ֱ��DNƽ���߶�QF��
���� ���⿼���˷���������ͼ���ϵ�����������������б�ʽ������ϵ���Ĺ�ϵ��ƽ���ߵ������Լ������ľ��빫ʽ������Ĺؼ��ǣ���1�����÷���������ͼ���ϵ������������������������Ľ���ʽ����2���ɹ���k��һԪ���η�����ó������ڣ���3��ͨ��������ϵ�ҳ�FK=QK�����������е��⣬�ѶȲ������и����������ο���ʽ��Ϊ���ǽ�������˷��㣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
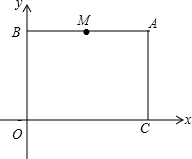 ƽ��ֱ������ϵ�У�O������ԭ�㣬��A�ǵ�һ������һ�㣬A��m��n������$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$����A�ֱ���x���y���ƽ���ߣ���y���ڵ�B����x���ڵ�C��M���߶�AB���е㣬��P��M��������߶�MA-AC���յ�C�˶����ٶ�Ϊÿ��2����λ���ȣ����P�˶���ʱ��Ϊt���룩��
ƽ��ֱ������ϵ�У�O������ԭ�㣬��A�ǵ�һ������һ�㣬A��m��n������$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$����A�ֱ���x���y���ƽ���ߣ���y���ڵ�B����x���ڵ�C��M���߶�AB���е㣬��P��M��������߶�MA-AC���յ�C�˶����ٶ�Ϊÿ��2����λ���ȣ����P�˶���ʱ��Ϊt���룩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��6 | B�� | x��-6 | C�� | x��-6 | D�� | x��-6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com