
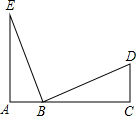
 如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请依据ASA,添加一个适当的条件AE=EB,使得△EAB≌△BCD.
如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请依据ASA,添加一个适当的条件AE=EB,使得△EAB≌△BCD.  亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
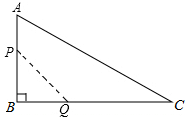 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
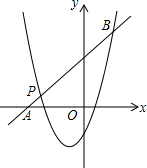 已知二次函数y1=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.
已知二次函数y1=x2+mx+n的图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴的直线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.0<AB<3.1 | B. | 3.1<AB<3.2 | C. | 3.2<AB<3.3 | D. | 3.3<AB<3.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com