
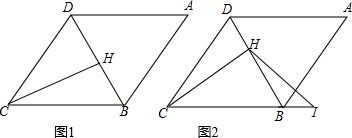
分析 (1)由在菱形ABCD中,∠A=60°,易得△BCD是等边三角形,又由H是线段BD的中点,且AB=6,可得CH⊥BD,BD=BC=6,继而求得CH的长,则可求得△DBC的面积;
(2)首先过点H作GH∥BC,交CD于点G,易得△DGH是等边三角形,则可得CG=BH,GH=BI,∠CGH=∠HBI=120°,则可证得△CGH≌△HBI(SAS),继而证得结论.
解答 解:(1)∵四边形ABCD是菱形,
∴BC=DC,∠BCD=∠A=60°,BC=AB=6,
∴△BCD是等边三角形,
∴BD=BC=6,
∵H是线段BD的中点,
∴BH=$\frac{1}{2}$BD=3,CH⊥BD,
∴CH=$\sqrt{B{C}^{2}-B{H}^{2}}$=3$\sqrt{3}$,
∴S△DBC=$\frac{1}{2}$BD•CH=9$\sqrt{3}$;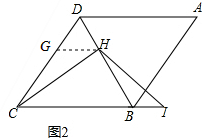 (2)过点H作GH∥BC,交CD于点G,
(2)过点H作GH∥BC,交CD于点G,
∵△BCD是等边三角形,
∴∠DHG=∠DBC=60°,∠DGH=∠DCB=60°,CD=BD,
∴△DGH是等边三角形,
∴DH=DG=GH,∠DGH=∠DBC=60°,
∴CG=HB,∠CGH=∠HBI,
∵DH=BI,
∴GH=BI,
在△CGH和△HBI中,
$\left\{\begin{array}{l}{CG=HB}\\{∠CGH=∠HBI}\\{GH=BI}\end{array}\right.$,
∴△CGH≌△HBI(SAS),
∴CH=HI.
点评 此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com