
 =30�㣬OEΪ��BOD�����ߣ���B��E�����������y=ax2-
=30�㣬OEΪ��BOD�����ߣ���B��E�����������y=ax2- x+c��x���ཻ��A��F���㣨A��F���Ҳࣩ��
x+c��x���ཻ��A��F���㣨A��F���Ҳࣩ�� ��
�� ��1����
��1���� x+c����B��0��2����E��-
x+c����B��0��2����E��- ��1����
��1����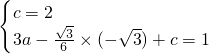 ��
��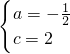 ��
�� x2-
x2- x+2��
x+2�� ��0����
��0���� x+2��
x+2�� ��1����
��1���� x��
x�� x2-
x2- x+2=1��
x+2=1�� ��Ϊ��E����ȥ����x2=
��Ϊ��E����ȥ����x2= ��
�� ��1����
��1���� x+m��
x+m�� ����-2
����-2 ��+m=0��
��+m=0�� x-2��
x-2��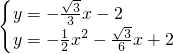 ��
��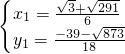 ��
��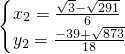 ��
��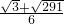 ��
��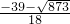 ����
����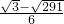 ��
��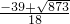 ����
���� x��
x��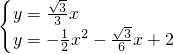 ��
��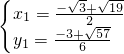 ��
��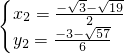 ��
�� ��
��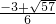 ����
����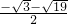 ��
�� ����
���� ��1����P2��
��1����P2��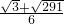 ��
��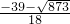 ����P3��
����P3��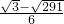 ��
��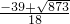 ����P4��
����P4�� ��
��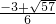 ����P5��
����P5��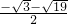 ��
�� ����
���� x2-
x2- x+2=0��
x+2=0�� x+12=0��
x+12=0��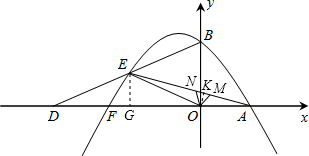
 ��x2=
��x2= ��
�� ��0����
��0���� ��1����
��1���� ��EG=1��
��EG=1�� +
+ =2
=2 ��
��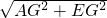 =
=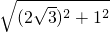 =
= ��
�� =
= ��
��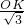 =
=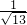 ��
��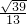 ��
��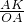 =
=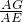 ��
��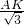 =
=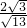 ��
��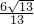 ��
��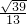 ��
�� =
=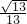 ��
��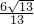 +
+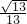 =
=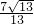 ��
��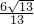 -
-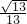 =
=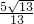 ��
��

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��| BD |
| AB |
| 5 |
| 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����| 5 |
| 29 |
| 5 |
| 29 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=| k |
| x |
| k |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com