
 ,所以GR=3-
,所以GR=3- ,
, ),
), )=2
)=2 -3
-3

 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠·优化训练(冀教版)七年级数学(下) 冀教版银版 题型:044
如图所示是边长分别为:2a+b,a+b,a-b的长方体.
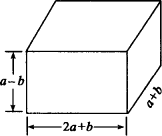
(1)求它的体积.
(2)求它的表面积.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江绍兴杨汛桥镇中学八年级上单元检测数学试题(带解析) 题型:解答题
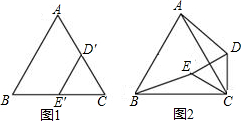
如图1,是边长分别为5和2的两个等边三角形纸片ABC和CDˊEˊ叠放在一起.
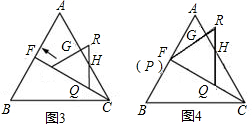
(1)操作:固定△ABC,将△CDˊEˊ绕点C顺时针旋转得到△CDE,连结AD、BE,如图2.探究:在图2中,线段BE与AD之间有怎样的大小关系?试说明理由;
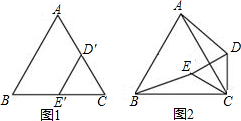
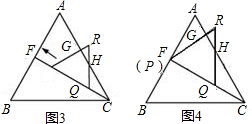
(2)操作:固定△ABC,若将△CDˊEˊ绕点C顺时针旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于点F,在线段CF上沿着CF方向以每秒1个单位长的速度平移,平移后的△CDE设为△PQR,如图3.探究:在图3中,除△ABC和△PQR外,还有哪个三角形是等腰三角形?写出你的结论并说明理由;
(3)探究:如图3,在(2)的条件下,设△PQR移动的时间为1秒,求△PQR与△AFC重叠部分的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com