
【题目】点![]() 在同一直线上,点
在同一直线上,点![]() 位于
位于![]() 的同侧,连接
的同侧,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
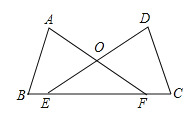
(1)如图1,求证:![]() ;
;
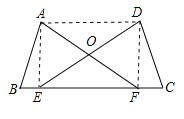
(2)如图2,连接![]() ,请直接写出图中所有的全等三角形(
,请直接写出图中所有的全等三角形(![]() 除外)
除外)
【答案】(1)证明见详解;(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据边与边的关系可找出BF=CE,再结合AB=DC,∠B=∠C,即可证出△ABF≌△DCE(SAS),从而可得出∠OEF=∠OFE,AF=DE,进而得出OE=OF,OA=OD,此题得证;
(2)由(1)可知△ABF≌△DCE,![]() ,
,![]() ,根据相等的边角关系可证出△AOE≌△DOF(SAS),△ABE≌△DCF(SAS),△AEF≌△DFE(SAS),△AED≌△DFA(SSS).
,根据相等的边角关系可证出△AOE≌△DOF(SAS),△ABE≌△DCF(SAS),△AEF≌△DFE(SAS),△AED≌△DFA(SSS).
(1)![]()
![]()
![]()
![]()
![]() (SAS)
(SAS)
![]()
![]()
![]()
![]()
(2)解:如图2所示,
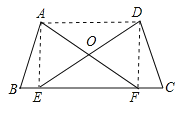
由(1)可知△ABF≌△DCE,![]() ,
,![]() ;
;
在△AOE和△DOF中,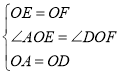
∴△AOE≌△DOF(SAS),;
在△ABE和△DCF中,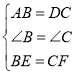
∴△ABE≌△DCF(SAS),
∴![]() ;
;
由(1)知![]()
在△AEF和△DFE中,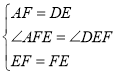
∴△AEF≌△DFE(SAS);
在△AED和△DFA中,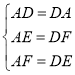
∴△AED≌△DFA(SSS);
故全等的三角形有:
![]()


科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子1张或椅子4把,现计划用120块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.
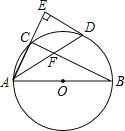
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的开口向下与
的开口向下与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点(不与点
是抛物线上一个动点(不与点![]() 重合)
重合)

(1)求抛物线的解析式;
(2)当点![]() 是抛物线上一个动点,若
是抛物线上一个动点,若![]() 的面积为12,求点
的面积为12,求点![]() 的坐标;
的坐标;
(3)如图2,抛物线的顶点为![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() ,若存在请直接写出点
,若存在请直接写出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
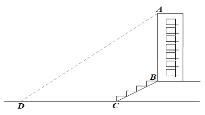
【题目】某班的同学想测量一教楼AB的高度.如图,大楼前有一段斜坡![]() ,已知
,已知![]() 的长为16米,它的坡度
的长为16米,它的坡度![]() .在离
.在离![]() 点45米的
点45米的![]() 处,测得一教楼顶端
处,测得一教楼顶端![]() 的仰角为
的仰角为![]() ,则一教楼
,则一教楼![]() 的高度约( )米(结果精确到0.1米)(参考数据:
的高度约( )米(结果精确到0.1米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
A. 44.1 B. 39.8 C. 36.1 D. 25.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com