
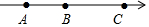 ��ͼ����֪������A���ʾ��a��B���ʾ��b��C���ʾ��c��
��ͼ����֪������A���ʾ��a��B���ʾ��b��C���ʾ��c������ ��1�����ݷǸ������������a=-3��b=9��
��2����C�����߶�AB�Ϻ��߶�AB���ӳ���������������ۼ�����⣻
��3����P���B�غ�ʱ��|x-a|+|x-b|+|x-c|����x=bʱ��ȡ����Сֵ��
��4���ֵ�0��t��4ʱ����t��4ʱ����ʾ���ס�����С��֮��ľ���d���ɣ�
��� �⣺��1����|a+3|+��c-9��2=0��
��a+3=0��c-9=0��
��ã�a=-3��b=9��
�ʴ�Ϊ��-3��9��
��2�������ϵ�B��ʾ����Ϊb��
��BC=2AB��
��|c-b|=2|b-a|��
��9-b=2[b-��-3��]
��ã�b=1��
�ʴ�Ϊ��1��
��3����x=b=1ʱ��
|x-a|+|x-b|+|x-c|=|x-��-3��|+|x-1|+|x-9|=12Ϊ��Сֵ��
�ʴ�Ϊ��12��
��4����t������4�루�����Ϊ0��t��4��4����ǰ����d=12-t��
��t����4�루�����Ϊt��4��4���Ժ�d=3t-4��
���� ���⿼������ʽ�ļӼ����д���ʽ�����ᡢ�Ǹ��������ʡ�����������֮��ľ��룬��������֮��ľ������ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 4 | C�� | 2 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
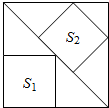 ��ͼ���߳�Ϊ6�Ĵ���������������С�����Σ�������С�����ε�����ֱ�ΪS1��S2����S1+S2��ֵΪ17��
��ͼ���߳�Ϊ6�Ĵ���������������С�����Σ�������С�����ε�����ֱ�ΪS1��S2����S1+S2��ֵΪ17���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��1+x%��2=a | B�� | a��1-x%��2=b | C�� | a��1+x%��2=b | D�� | a��1-2x%��=b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 21 | B�� | 26 | C�� | 29 | D�� | 21��29 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2��y3 | B�� | y2��y1��y3 | C�� | y3��y1��y2 | D�� | y1��y3��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7cm��8cm��15cm | B�� | 15cm��20cm��5cm | C�� | 6cm��7cm��5cm | D�� | 7cm��6cm��14cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���κ���y=ax2+bx+c��a��0����ͼ����ͼ���Գ�����x=1�����н��ۣ�
���κ���y=ax2+bx+c��a��0����ͼ����ͼ���Գ�����x=1�����н��ۣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com