
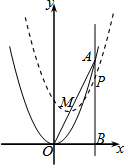
 如图,直线x=2上有一点A(2,4),将抛物线y=x2的顶点在线段OA上移动到M,得到
如图,直线x=2上有一点A(2,4),将抛物线y=x2的顶点在线段OA上移动到M,得到分析 (1)根据A点的坐标,用待定系数法即可求出直线OA的解析式;
(2)由于M点在直线OA上,可根据直线OA的解析式来表示出M点的坐标,因为M点是平移后抛物线的顶点,因此可用顶点式二次函数通式来设出这个二次函数的解析式,P的横坐标为2,将其代入抛物线的解析式中即可得出P点的坐标,PB的长,实际就是P点的纵坐标,因此可根据其纵坐标的表达式来求出PB最短时,对应的m的值,即可得到结论;
(3)根据(2)中确定的m值可知:M、P点的坐标都已确定,因此AM的长为定值,若要使△QMA的面积与△PMA的面积相等,那么Q点到AM的距离和P到AM的距离应该相等,因此可分两种情况进行讨论:
①当Q在直线OA下方时,可过P作直线OA的平行线交y轴于C,那么平行线上的点到OA的距离可相等,因此Q点必落在直线PC上,可先求出直线PC的解析式,然后利用抛物线的解析式,看得出的方程是否有解,如果没有则说明不存在这样的Q点,如果有解,得出的x的值就是Q点的横坐标,可将其代入抛物线的解析式中得出Q点的坐标.
②当Q在直线OA上方时,同①类似,可先找出P关于A点的对称点D,过D作直线OA的平行线交y轴于E,那么直线DE上的点到AM的距离都等于点P到AM上的距离,然后按①的方法进行求解即可.
解答 解:(1)设直线OA的解析式为y=kx,
把点A坐标(2,4)代入得,4=2k,
∴k=2,
∴直线OA的解析式为y=2x;
(2)∵顶点M的横坐标为m,且点M在直线OA上,
∴顶点M的坐标为(m,2m),
∴抛物线的解析式为y=(x-m)2+2m,
当x=2时,y=(2-m)2+2m=m2-2m+4(0≤x≤2),
∴点P的坐标为(2,m2-2m+4),
PB=m2-2m+4=(m-1)2+3,
∵0≤x≤2,当m=1时,PB最短,
即:点P到x轴的最短距离是3;
(3)当PB最短时,抛物线的解析式为y=(x-1)2+2,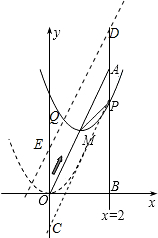
假设抛物线上存在点Q,使△QMA的面积与△PMA的面积相等,
设Q(x,x2-2x+3),
①当点Q在直线OA的下方时,过点P作直线PC∥AO,交y轴于点C,
∵PB=3,AB=4,
∴AP=1,
∴OC=1,
∴点C的坐标为(0,-1),
∵点P的坐标为(2,3),
∴直线PC的解析式为y=2x-1,
∵△QMA的面积与△PMA的面积相等,
∴点Q在直线PC上,
∴x2-2x+3=2x-1,解得x1=x2=2,即点Q(2,3),
∴与点P重合,所以这样的点Q不存在.
②当点Q落在直线OA的上方时,
作点P关于点A的对称称点D,过D作直线DE∥AO,交y轴于点E,
∵AP=1,
∴EO=DA=1,
∴E、D的坐标分别是(0,1),(2,5),
∴直线DE函数解析式为y=2x+1.
∵S△QMA=S△PMA,
∴点Q落在直线y=2x+1上.
∴x2-2x+3=2x+1.
解得:x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$.
代入y=2x+1得:y1=5+2$\sqrt{2}$,y2=5-2$\sqrt{2}$.
∴此时抛物线上存在点Q1(2+$\sqrt{2}$,5+2$\sqrt{2}$),Q2(2-$\sqrt{2}$,5-2$\sqrt{2}$)
使△QMA与△PMA的面积相等.
综上所述,抛物线上存在点,Q1(2+$\sqrt{2}$,5+2$\sqrt{2}$),Q2(2-$\sqrt{2}$,5-2$\sqrt{2}$)使△QMA与△PMA的面积相等.
点评 本题考查了一次函数解析式的确定、二次函数图象的平移、函数图象的交点、图形面积的求法等知识点,主要考查学生分类讨论和数形结合的数学思想方法.


科目:初中数学 来源: 题型:解答题
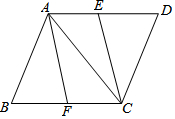 如图,在?ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.
如图,在?ABCD中,E、F分别是AD、BC的中点,连接AC、CE、AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
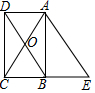 如图,矩形ABCD的对角线AC与BD相交于点O,延长CB至点E,使BE=BC,连按AE.
如图,矩形ABCD的对角线AC与BD相交于点O,延长CB至点E,使BE=BC,连按AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com