
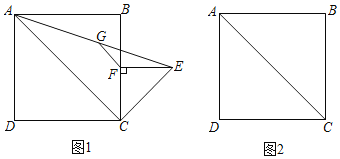
【题目】已知如图1,正方形ABCD,△CEF为等腰直角三角形,其中∠CFE=90°,CF=EF,连接CE,AE,AC,点G是AE的中点,连接FG
(1)用等式表示线段BF与FG的数量关系是 .
(2)若将△CEF绕顶点C旋转,使得点F恰好在线段AC上,并且点E在线段AC的上方,点G仍是AE的中点,连接FG,DF
①在图2中依据题意补全图形;
②求证:DF=![]() FG.
FG.
【答案】(1)BF=![]() FG;(2)①见解析;②见解析.
FG;(2)①见解析;②见解析.
【解析】
(1)先判断出△AGB≌△CGB,得到∠GBF=45°,再判断出△EFG≌△CFG,得到∠GFB=45°,从而得到△BGF为等腰直角三角形,即可求解;
(2)①按题意画图2即可;
②如图2,连接BF、BG,证明△ADF≌△ABF得DF=BF,根据直角三角形斜边中线的性质得:AG=EG=BG=FG,由圆的定义可知:点A、F、E、B在以点G为圆心,AG长为半径的圆上,∠BGF=2∠BAC=90°,所以△BGF是等腰直角三角形,可得结论.
(1)BF=![]() FG,
FG,
理由是:如图1,连接BG,CG,

∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
∵EF⊥BC,FE=FC,
∴∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∵BG=BG,
∴△AGB≌△CGB(SSS),
∴∠ABG=∠CBG=![]() ∠ABC=45°,
∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG(SSS),
∴∠EFG=∠CFG=![]() (360°﹣∠BFE)=
(360°﹣∠BFE)=![]() (360°﹣90°)=135°,
(360°﹣90°)=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=![]() FG.
FG.
故答案为:BF=![]() FG;
FG;
(2)①如图2所示,

②如图2,连接BF、BG,
∵四边形ABCD是正方形,
∴AD=AB,∠ABC=∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠DAC=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS),
∴DF=BF,
∵EF⊥AC,∠ABC=90°,点G是AE的中点,
∴AG=EG=BG=FG,
∴点A、F、E、B在以点G为圆心,AG长为半径的圆上,
∵![]() ,∠BAC=45°,
,∠BAC=45°,
∴∠BGF=2∠BAC=90°,
∴△BGF是等腰直角三角形,
∴BF=![]() FG,
FG,
∴DF=![]() FG.
FG.


科目:初中数学 来源: 题型:
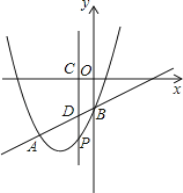
【题目】如图,抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点.点A的横坐标为﹣3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,S四边形OBDC=2S△BPD;
(3)是否存在点P,使△PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市园林处为了对一段公路进行绿化,计划购买![]() ,
,![]() 两种风景树共900棵.
两种风景树共900棵.![]() ,
,![]() 两种树的相关信息如下表:
两种树的相关信息如下表:
品种 项目 | 单价(元 | 成活率 |
| 80 |
|
| 100 |
|
若购买![]() 种树
种树![]() 棵,购树所需的总费用为
棵,购树所需的总费用为![]() 元.
元.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若购树的总费用不超过82 000元,则购![]() 种树不少于多少棵?
种树不少于多少棵?
(3)若希望这批树的成活率不低于![]() ,且使购树的总费用最低,应选购
,且使购树的总费用最低,应选购![]() ,
,![]() 两种树各多少棵?此时最低费用为多少?
两种树各多少棵?此时最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
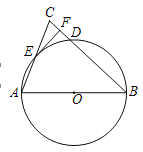
【题目】已知:在△ABC中,AB=BC,以AB为直径作![]() ,交BC于点D,交AC于E,过点E作
,交BC于点D,交AC于E,过点E作![]() 切线EF,交BC于F.
切线EF,交BC于F.
(1)求证:EF⊥BC;
(2)若CD=2,tanC=2,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
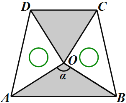
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
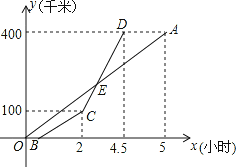
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎做一道数学题,“已知两个多项式![]() ,
,![]() ,试求
,试求![]() .”其中多项式
.”其中多项式![]() 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.
(1)小马虎看答案以后知道![]() ,请你替小马虎求出系数“
,请你替小马虎求出系数“![]() ”;
”;
(2)在(1)的基础上,小马虎已经将多项式![]() 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式![]() ,要求小马虎求出
,要求小马虎求出![]() 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“![]() ”看成“
”看成“![]() ”,结果求出的答案为
”,结果求出的答案为![]() .请你替小马虎求出“
.请你替小马虎求出“![]() ”的正确答案.
”的正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
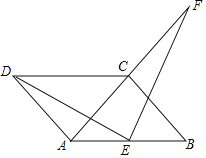
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com