
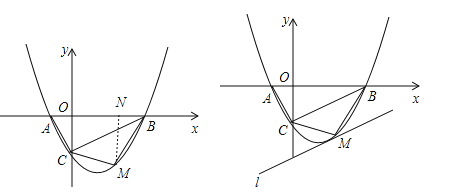
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

【答案】(1)![]() ;(2)(
;(2)(![]() ,0);(3)4,M(2,﹣3).
,0);(3)4,M(2,﹣3).
【解析】试题分析:方法一:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
(3)△MBC的面积可由S△MBC=![]() BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
方法二:
(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)通过求出A,B,C三点坐标,利用勾股定理或利用斜率垂直公式可求出AC⊥BC,从而求出圆心坐标.
(3)利用三角形面积公式,过M点作x轴垂线,水平底与铅垂高乘积的一半,得出△MBC的面积函数,从而求出M点.
试题解析:解:方法一:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,即:OC2=OAOB,又:OC⊥AB,∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,∴△ABC为直角三角形,AB为△ABC外接圆的直径;
所以该外接圆的圆心为AB的中点,且坐标为:(![]() ,0).
,0).
(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为:y=![]() x﹣2;
x﹣2;
设直线l∥BC,则该直线的解析式可表示为:y=![]() x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b,当直线l与抛物线只有一个交点时,可列方程:
![]() x+b=
x+b=![]() ,即:
,即: ![]() ,且△=0;
,且△=0;
∴4﹣4×![]() (﹣2﹣b)=0,即b=﹣4;
(﹣2﹣b)=0,即b=﹣4;
∴直线l:y=![]() x﹣4.
x﹣4.
所以点M即直线l和抛物线的唯一交点,有:  ,解得:
,解得: ![]()
即 M(2,﹣3).
过M点作MN⊥x轴于N,S△BMC=S梯形OCMN+S△MNB﹣S△OCB=![]() ×2×(2+3)+
×2×(2+3)+![]() ×2×3﹣
×2×3﹣![]() ×2×4=4.
×2×4=4.
方法二:
(1)将B(4,0)代入抛物线的解析式中,得: 0=16a﹣![]() ×4﹣2,即:a=
×4﹣2,即:a=![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() .
.
(2)∵y=![]() (x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=
(x﹣4)(x+1),∴A(﹣1,0),B(4,0).C(0,﹣2),∴KAC=![]() =﹣2,KBC=
=﹣2,KBC=![]() =
=![]() ,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(
,∴KAC×KBC=﹣1,∴AC⊥BC,∴△ABC是以AB为斜边的直角三角形,△ABC的外接圆的圆心是AB的中点,△ABC的外接圆的圆心坐标为(![]() ,0).
,0).
(3)过点M作x轴的垂线交BC′于H,∵B(4,0),C(0,﹣2),∴lBC:y=![]() x﹣2,设H(t,
x﹣2,设H(t, ![]() t﹣2),M(t,
t﹣2),M(t, ![]() ),∴S△MBC=
),∴S△MBC=![]() ×(HY﹣MY)(BX﹣CX)=
×(HY﹣MY)(BX﹣CX)=![]() ×(
×(![]() t﹣2﹣
t﹣2﹣![]() )(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).
)(4﹣0)=﹣t2+4t,∴当t=2时,S有最大值4,∴M(2,﹣3).

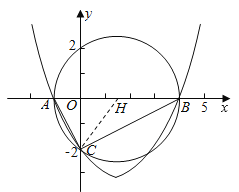


科目:初中数学 来源: 题型:
【题目】某体育用品制造公司通过互联网销售某品牌排球,第一周的总销售额为3000元,第二周的总销售额为3520元,第二周比第一周多售出13个排球.
(1)求每个排球的售价;
(2)该公司在第三周将每个排球的售价降低了![]() (其中
(其中![]() ),并预计第三周能售出120个排球.恰逢中国女排夺冠,极大地激发了广大青少年积极参与排球运动的热情,该款排球在第三周的销量比预计的120个还多了
),并预计第三周能售出120个排球.恰逢中国女排夺冠,极大地激发了广大青少年积极参与排球运动的热情,该款排球在第三周的销量比预计的120个还多了![]() .已知每个排球的成本为16元,该公司第三周销售排球的总利润为4320元,求
.已知每个排球的成本为16元,该公司第三周销售排球的总利润为4320元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是推导“三角形内角和定理”的学习过程,请补全证明过程及推理依据.

已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
证明:过点A作DE∥BC,(请在图上画出该辅助线并标注D,E两个字母)
∠B=∠BAD,∠C= .( )
∵点D,A,E在同一条直线上,
∴ (平角的定义)
∴∠B+∠BAC+∠C=180°
即三角形的内角和为180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(操作发现)
如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为 B′,点 C 的对应点为 C′, 连接 BB′,如图所示则∠AB′B= .
(2)(解决问题)
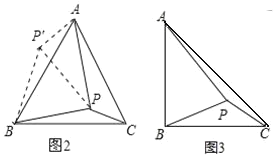
如图 2,在等边ABC 内有一点 P,且 PA=2,PB=![]() ,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
(3)(灵活运用)
如图 3,将(2)题中“在等边ABC 内有一点 P 改为“在等腰直角三角形 ABC 内有一点P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,![]() 的三个顶点均在格点上,请按要求完成下列各题:
的三个顶点均在格点上,请按要求完成下列各题:

(1)画线段![]() ,且使
,且使![]() ,连接
,连接![]() ;
;
(2)线段![]() 的长为________,
的长为________,![]() 的长为________,
的长为________,![]() 的长为________;
的长为________;
(3)![]() 是________三角形,四边形
是________三角形,四边形![]() 的面积是________;
的面积是________;
(4)若点![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() ,则
,则![]() 的度数为________.
的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:

(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单 位:s)(0<t<![]() )。
)。
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,已知该小区用水量不超过![]() 的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
级别 |
|
|
|
|
|
|
月均用水量 |
|
|
|
|
|
|
频数(户) | 6 | 12 |
| 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)补全频率分布直方图;

(3)若将调查数据绘制成扇形统计图,则月均用水量“![]() ”的圆心角度数是 .
”的圆心角度数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com