
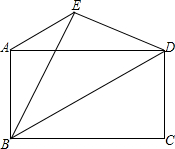
 如图,已知矩形ABCD,把矩形ABCD沿直线BD翻折,点C落在点E处,连接AE.
如图,已知矩形ABCD,把矩形ABCD沿直线BD翻折,点C落在点E处,连接AE.分析 (1)根据矩形的性质得AD=BC=$\sqrt{6}$,AB=DC=$\sqrt{3}$,AD∥BC,根据勾股定理可计算出BD=3,再根据折叠的性质得∠DBC=∠DBE,BE=BC=$\sqrt{6}$,ED=DC=$\sqrt{3}$,则∠DBE=∠ADB,所以BF=DF,又AD=BE,则AF=EF,所以∠DAE=∠AEB,于是∠DAE=∠AEB=∠DBE=∠ADB,得到BD∥AE,而AB=DE=$\sqrt{3}$,且AB与DE不平行,所以可判断四边形ABDE是等腰梯形,过点A、E分别作AM⊥BD于点M、EN⊥BD于点N,则四边形AMNE为矩形,根据等腰图形的性质易得BM=DN,AE=MN,在Rt△ABD中,利用面积法克计算出AM=$\frac{\sqrt{6}×\sqrt{3}}{3}$=$\sqrt{2}$,在Rt△ABM中,利用勾股定理计算出BM=1,则AE=MN=3-1=2,然后根据梯形的面积公式求解;
(2)利用(1)中的结论,作PM⊥BD于点M,得出PM=$\frac{1}{2}$BD,进一步证得△DPM∽△BDC,利用性质求得结论即可.
解答 解:(1)如图,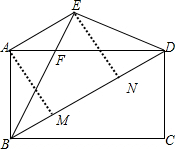
设BE与AD交于点F.
∵四边形ABCD为矩形,AB=$\sqrt{3}$,BC=$\sqrt{6}$,
∴AD=BC=$\sqrt{6}$,AB=DC=$\sqrt{3}$,AD∥BC,
∴BD=3,∠DBE=∠ADB,
∵把矩形ABCD沿对角线BD折叠,使点C落在点E处,
∴∠DBC=∠DBE,BE=BC=$\sqrt{6}$,ED=DC=$\sqrt{3}$,
∴∠FBD=∠FDB,
∴BF=DF,
∵BE=AD,
∴EF=AF,
∴∠FAE=∠FEA,
∴∠DAE=∠AEB=∠DBE=∠ADB,
∴AE∥BD,
∵AB=DE=$\sqrt{3}$,且AB与DE不平行,
∴四边形ABDE是等腰梯形.
过点A、E分别作AM⊥BD于点M、EN⊥BD于点N,则四边形AMNE为矩形,
∴BM=DN,AE=MN,
在Rt△ABD中,$\frac{1}{2}$AM•BD=$\frac{1}{2}$AD•AB,则AM=$\frac{\sqrt{3}×\sqrt{6}}{3}$=$\sqrt{2}$,
在Rt△ABM中,BM=1,
∴DN=1,
∴AE=MN=3-1-1=1,
∴梯形ABDE的面积=$\frac{1}{2}$(AE+BD)•AM=2$\sqrt{2}$.
(2)如图,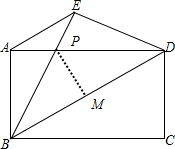
作PM⊥BD,垂足为点M,
由(1)可知BM=DM=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$,
∵∠PMD=∠C,∠PDM=∠DBC,
∴△DPM∽△BDC,
∴$\frac{PD}{BD}$=$\frac{DM}{BC}$
∴$\frac{PD}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{\frac{1}{2}\sqrt{{a}^{2}+{b}^{2}}}{b}$
∴PD=$\frac{{a}^{2}+{b}^{2}}{2b}$.
点评 此题考查折叠的性质,矩形的性质,勾股定理,等腰梯形的判定与性质,相似三角形的判定与性质,题目综合性较强,注意条件的灵活运用,结合图形,正确做出辅助线解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解放碑泰兴电脑城某店在1~10月份销售A、B两种电子产品,已知A产品每月的售价y(元)与月份x(1≤x≤10且x为整数)之间的关系可用如下表格表示:
解放碑泰兴电脑城某店在1~10月份销售A、B两种电子产品,已知A产品每月的售价y(元)与月份x(1≤x≤10且x为整数)之间的关系可用如下表格表示:| 时间x(月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 售价y(元) | 720 | 360 | 240 | 180 | 144 | 120 | 120 | 120 | 120 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com