练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点（-1，-2），“马”位于点（2，-2），则“兵”位于点（　　）
    A．（-1，1）B．（-2，-1）C．（-3，1）D．（1，-2）

    分析 直接利用“帅”位于点（-1，-2），可得原点的位置，进而得出“兵”的坐标．

    解答 解：如图所示：可得“炮”是原点，
    则“兵”位于点：（-3，1）．
    故选：C．

    点评 此题主要考查了坐标确定位置，正确得出原点的位置是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

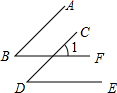    13．如图所示，AB∥CD，∠B=∠D，求证：BF∥DE（请在括号或横线上填空）
    证明：∵AB∥CD（已知）
    ∴∠B=∠1（（两直线平行，同位角相等）
    ∵∠B=∠D（已知）
    ∴∠1=∠D（等量代换）
    ∴BF∥DE（同位角相等，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．问题提出
    平面上，若点P与A、B、C三点中的任意两点均构成等腰三角形，则称点P是A、B、C三点的巧妙点．若A、B、C三点构成三角形，也称点P是△ABC的巧妙点．
    初步思考
    （1）如图①，在等边△ABC的内部和外部各作一个△ABC的巧妙点．（尺规作图，不写作法，保留作图痕迹）
    （2）如图②，在△ABC中，AB=AC，∠BAC=36°，点D、E是△ABC的两个巧妙点，其中AD=AB，AE=AC，BD=BC=CE，连接DE，分别交AB、AC于点M、N．求证：DA2=DB•DE．
    深入研究
    （3）在△ABC中，AB=AC，若存在一点P，使PB=BA，PA=PC．点P可能为△ABC的巧妙点吗？若可能，请画出示意图，并直接写出∠BAC的度数；若不可能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．若关于x的一元二次方程x2-4x-k=0有两个实数根，则（　　）
    A．k＞4B．k＞-4C．k≥4D．k≥-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．化简：
    （1）3$\sqrt{3}$-（$\sqrt{12}$+$\sqrt{\frac{1}{3}}$）
    （2）（$\sqrt{18}$-$\sqrt{24}$）÷$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解方程组
    （1）$\left\{\begin{array}{l}{3x+2y=19}\\{2x-y=1}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{4（x+y）-5（x-y）=2}\\{\frac{x+y}{2}+\frac{x-y}{3}=6}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列说法错误的是（　　）
    A．相等的角是对顶角
    B．同角的补角相等
    C．直线外一点与直线上各点连接的所有线段中，垂线段最短
    D．平行于同一条直线的两条直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．为了解九（3）班学生每天零花钱的使用情况，小明随机调查了20名同学，结果如表：关于这20名同学每天使用的零花钱，下列说法错误的是（　　）
    每天使用零花钱（单位：元）012345
    人数256421
    A．众数是2元B．中位数是2元C．极差是5元D．平均数是2.45元

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图1，矩形ABCD中，AB=8，BC=8$\sqrt{3}$，半径为$\sqrt{3}$的⊙P与线段BD相切于点M，圆心P与点C在直线BD的同侧，⊙P沿线段BD从点B向点D滚动．
    发现：BD=16；∠CBD的度数为30°；
    拓展：
    ①当切点M与点B重合时，求⊙P与矩形ABCD重叠部分的面积；
    ②在滚动过程中如图2，求AP的最小值；
    探究：
    ①若⊙P与矩形ABCD的两条对角线都相切如图3，求此时线段BM的长，并直接写出tan∠PBC的值；
    ②在滚动过程中如图4，点N是AC上任意一点，直接写出BP+PN的最小值．

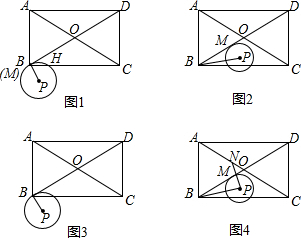
    查看答案和解析>>

    同步练习册答案