
【题目】如图1,直线![]() x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,将△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,将△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
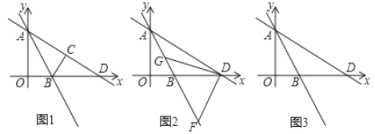
(1)求OB的长;
(2)如图2,F,G是直线AB上的两点,若△DFG是以FG为斜边的等腰直角三角形,求点F的坐标;
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P,Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
【答案】(1)OB=3;(2)F(6,-6);(3)E(-2,0).
【解析】
(1)设BC=OB=x,则BD=8-x,在Rt△BCD中,根据![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)作GM⊥x轴于M,FN⊥x轴于N,由△DMG≌△FND(AAS),推出GM=DN,DM=FN,设GM=DM=m,DM=FN=n,根据G、F在直线AB上,构建方程组即可解决问题;
(3)如图,设Q![]() ,因为PQ∥x轴,且点P在直线y=-2x+6上,推出P
,因为PQ∥x轴,且点P在直线y=-2x+6上,推出P![]() ,PQ=
,PQ=![]() ,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,构建方程即可解决问题.
,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,构建方程即可解决问题.
解:(1)对于直线![]() ,令x=0,得到y=6,可得A(0,6),
,令x=0,得到y=6,可得A(0,6),
令y=0,得到x=8,可得D(8,0),
![]() AC=AO=6,OD=8,AD
AC=AO=6,OD=8,AD![]() ,
,
![]()
![]()
设BC=OB=x,则BD=![]() ,
,
在Rt△BCD中,∵BC2+CD2=BD2,
![]()
![]()
![]() x=3,
x=3,
![]() OB=3.
OB=3.
(2)设直线AB的解析式为y=kx+6(k≠0),
![]() OB=3,即B(3,0),
OB=3,即B(3,0),
![]() 把B(3,0)代入y=kx+6得,
把B(3,0)代入y=kx+6得,
![]() 3k+6=0,
3k+6=0,
![]()
![]() 直线AB的解析式为y=-2x+6,
直线AB的解析式为y=-2x+6,
作GM⊥x轴于M,FN⊥x轴于N,![]()
![]() △DFG是等腰直角三角形,
△DFG是等腰直角三角形,
![]() DG=FD,∠GDF=90°,
DG=FD,∠GDF=90°,
![]()
![]()
![]()
![]()
在△DMG和△FND中,

![]()
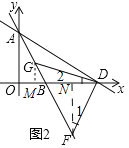
![]() GM=DN,DM=FN,设GM=DN=m,DM=FN=n,
GM=DN,DM=FN,设GM=DN=m,DM=FN=n,
![]()
![]() G、F在直线AB上,
G、F在直线AB上,
则: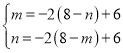 ,
,
解得:![]()
![]() ON=OD-DN=8-2=6,
ON=OD-DN=8-2=6,
![]()
![]()
![]() F(6,-6).
F(6,-6).
(3)如图,设Q(a,![]() ),
),
![]() PQ//x轴,且点P在直线
PQ//x轴,且点P在直线![]() 上,
上,
![]() P(
P(![]() ),
),
![]() PQ
PQ![]() ,作QH⊥x轴于H.
,作QH⊥x轴于H.
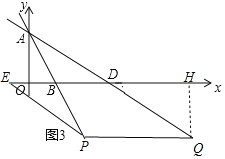
![]()
∴![]() ,
,
![]() ,
,
![]()
![]()
![]()
由勾股定理可知:QH:DH:DQ=3:4:5,
![]() 四边形PQDE为菱形,
四边形PQDE为菱形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Q(16,-6),P(6,-6),
Q(16,-6),P(6,-6),
![]()
![]()
![]()


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:m),如果在离水面竖直距离为h(单校:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H—h).
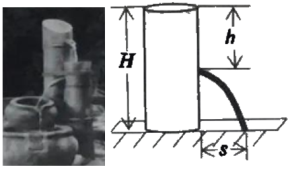
应用思考:现用高度为20cm的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连注水保证它始终盛满水,在离水面竖直距高h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16cm,求整高的高度及小孔离水面的竖直距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线y=2x+2和直线y=![]() x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2B.y=![]() x+2C.y=4x+2D.y=
x+2C.y=4x+2D.y=![]() x+2
x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
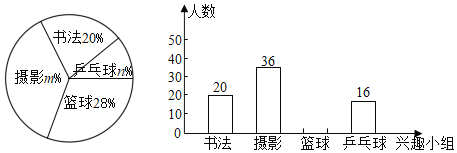
【题目】某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组,要求每人必须参加并且只能选择其中的一个小组,为了了解学生对四个课外小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的两幅不完整的统计图,请你根据给出的信息解答下列问题:
(1)求该校参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);
(2)m= ,n= ;
(3)若该校共有2000名学生,试估计该校选择“乒乓球”课外兴趣小组的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: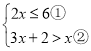 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(1)解不等式①,得: ;
(2)解不等式②得: ;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
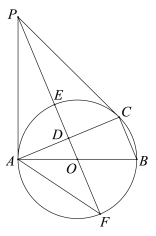
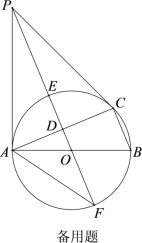
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
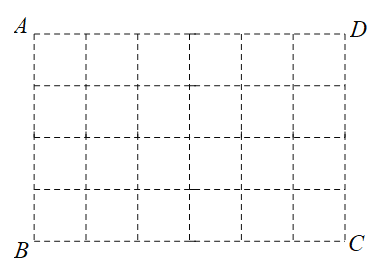
【题目】如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.
(1)在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH;
(2)在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
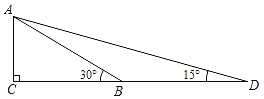
【题目】构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°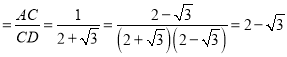 .类比这种方法,计算tan22.5°的值为( )
.类比这种方法,计算tan22.5°的值为( )
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
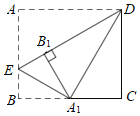
【题目】如图,在矩形ABCD中,E是AB上一点,将△ADE沿DE翻折,点A恰好落在BC上,记为A1,折痕为DE.再将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1.若AD=1,则AB的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com