【题目】如图，在四边形ABCD中，AC平分∠BAD，过C作CE⊥AB于E，并且AE＝
(AB＋AD)，求∠ABC＋∠ADC的度数．
【答案】180°
【解析】
延长AD过C作CF⊥AD于F，由条件可证△AFC≌△AEC，得到CF=CE．再由条件
可证BE=DF，所以△CDF≌△CEB，由全等的性质可得∠ABC=∠CDF，问题可得解．
过C作CF⊥AD于F．
∵AC平分∠BAD，∴∠FAC=∠EAC．
∵CE⊥AB，CF⊥AD，∴∠DFC=∠CEA=90°，∴△AFC≌△AEC（AAS），∴AF=AE，CF=CE．
∵，∴2AE=AB+AD．
又∵AD=AF﹣DF，AB=AE+BE，AF=AE，∴2AE=AE+BE+AE﹣DF，∴BE=DF．
∵∠DFC=∠CEB=90°，CF=CE，∴△CDF≌△CEB（SAS），∴∠ABC=∠CDF．
∵∠ADC+∠CDF=180°，∴∠ABC+∠ADC=180°．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】某学校开展课外体育活动，决定开设
:篮球、
:乒乓球、
:踢毽子、
:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种)，随机抽取了部分学生进行调查，并将调查结果绘成如甲、乙所示的统计图，请你结合图中信息解答下列问题.
(1)求出“最喜欢篮球”部分的扇形的圆心角度数；
(2)请把条形统计图补充完整；
(3)若该校有学生1000人，请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解饮料自动售货机的销售情况，有关部门从北京市所有的饮料自动售货机中随机抽取20台进行了抽样调查，记录下某一天各自的销售情况
单位：元
，并对销售金额进行分组，整理成如下统计表：
28，8，18，63，15，30，70，42，36，47，
25，58，64，58，55，41，58，65，72，30
销售金额x |
|
|
|
|
划记 |
|
| ______ | ______ |
频数 | 3 | 5 | ______ | ______ |
请将表格补充完整；
用频数分布直方图将20台自动售货机的销售情况表示出来，并在图中标明相应数据；
根据绘制的频数分布直方图，你能获取哪些信息？至少写出两条不同类型信息
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，A点的坐标为(0，4)，B点的坐标为(3，0)，C(a，b)为平面直角坐标系内一点，若∠ABC＝90°，且BA＝BC，求ab的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
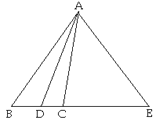
【题目】如图，AD平分∠BAC，∠EAD＝∠EDA.
（1）∠EAC与∠B相等吗？为什么？
（2）若∠B＝50°,∠CAD︰∠E＝1︰3，求∠E的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为方便市民出行，减轻城市中心交通压力，长沙市正在修建贯穿星城南北、东西的地铁1、2号线．已知修建地铁1号线24千米和2号线22千米共需投资265亿元；若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元．
（1）求1号线，2号线每千米的平均造价分别是多少亿元？
（2）除1、2号线外，长沙市政府规划到2018年还要再建91.8千米的地铁线网．据预算，这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍，则还需投资多少亿元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为cm2 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF． 求证：四边形BCFE是菱形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
