
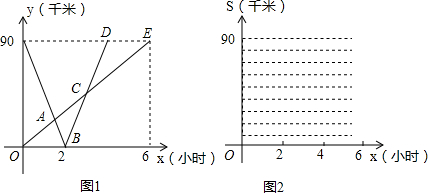
分析 (1)先求出B、D坐标,分0≤x≤2或2≤x≤4利用待定系数法分别求出y1,再利用待定系数法求出y2即可.
(2)分当0≤x≤1.5时,当1.5≤x≤2时,当2≤x≤3时,当3$≤x≤4\$时,当4≤x≤6时,分别构建一次函数即可解决问题.
(3)利用(2)的结论求出s=5时的x的值,再根据条件确定符合条件的x的范围.
解答 解:(1)由图1知摩托车的速度为:$\frac{90}{2}$=45(千米/小时),自行车的速度 $\frac{90}{6}$=15(千米/小时),
∴点B的坐标为(2,0),点D 的坐标为(4,90),
当0≤x≤2时,y1=90-45x,
当2≤x≤4时,y1=45x-90,
y2=15x,
(2)甲和乙在A点第一次相遇,时间t1=$\frac{90}{45+15}$=1.5小时,
甲和乙在C点第二次相遇,时间t2=$\frac{90}{45-15}$=3小时,.
当0≤x≤1.5时,s=y1-y2=-45x+90-15x=-60x+90,
∴x=1.5时,s=0,
当1.5≤x≤2时,s=y2-y1=15x-(-45x+90)=60x-90,
∴x=2时,s=30,
当2≤x≤3时,s=y2-y1=15x-(45x-90)=-30x+90,
∴x=3时,s=0,
当3$≤x≤4\$时,s=y1-y2=45x-90-15x=30x-90,
∴x=4时,s=30,
当4≤x≤6时,s=90-y2=90-15x,
∴x=6时,s=0,
故描出相应的点就可以补全图象. 如图所示,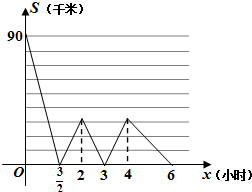
(3)∵0≤x≤1.5,s=-60x+90,s=5时,x=$\frac{17}{12}$,
1.5≤x≤2,s=-60x-90,s=5时,x=$\frac{19}{12}$,
2≤x≤3,s=-30x+90,s=5时,x=$\frac{17}{6}$,
3≤x≤4,s=30x-90,s=5时,x=$\frac{19}{6}$,
4≤x≤6,s=-1.5x+90,s=5时,x=$\frac{17}{3}$,
∴由图象知当两人距离不超过5千米时x的取值范围为:
$\frac{17}{12}$≤x≤$\frac{19}{12}$,$\frac{17}{6}$≤x≤$\frac{19}{6}$,$\frac{17}{3}$≤x≤6,
60×($\frac{19}{12}$-$\frac{17}{12}$)=10分钟,60×($\frac{19}{6}$-$\frac{17}{6}$)=20分钟,60×(6-$\frac{17}{3}$)=20分钟.
∴当两人能够用无线对讲机保持有效联系时x的取值范围为:
$\frac{17}{6}$≤x≤$\frac{19}{6}$,$\frac{17}{3}$≤x≤6.
点评 本题考查一次函数的应用、分段函数、待定系数法等知识,解题的关键是读懂图象信息,学会构建一次函数解决实际问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | m与4的差是负数,可表示为m-4<0 | B. | x不大于3可表示为x<3 | ||
| C. | a是负数可表示为a>0 | D. | x与2的和是非负数可表示为x+2>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
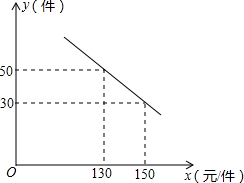 某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的商品,在商场试销发现:销售单价x(元/件)(100≤x≤160)与每天销售量y(件)之间满足如图所示的关系:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 2 | C. | -7 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
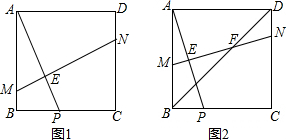
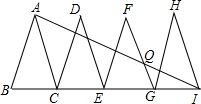 如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=$\frac{4}{3}$.
如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com