
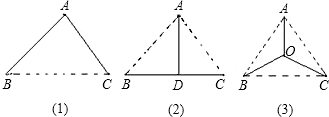
由于水资源缺乏,B,C两地不得不从黄河上的扬水站A处引水,这就需要在A,B,C之间铺设地下输水管道.有人设计了三种铺设方案:如图中的(1)(2)(3)所示,图中实线表示管道铺设线路,在图(2)中,AD^ BC;在图(3)中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路就尽量缩短.已知△ABC恰好是一边长为a的等边三角形,请你通过计算判断哪个铺设方案最好.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
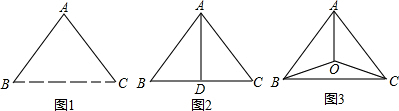
 .为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短.若△ABC恰好是一个边长为a的等边三角形,请你通过计算,判断哪一个铺设方案最好.
.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短.若△ABC恰好是一个边长为a的等边三角形,请你通过计算,判断哪一个铺设方案最好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com