
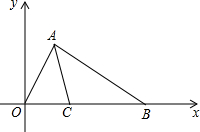
 如图,已知A(1,$\sqrt{3}$)、B(4,0),∠OAB的平分线AC交x轴于点C,试求线段OC的长度.
如图,已知A(1,$\sqrt{3}$)、B(4,0),∠OAB的平分线AC交x轴于点C,试求线段OC的长度. 分析 先由A(1,$\sqrt{3}$),B(4,0)求出OA,AB,通过勾股定理逆定理得△AOB为直角三角形且∠ABO=30°,再过点D作AO和AB的垂线分别交AO和AB于E、F,由∠OAB的平分线AC得CE=CF,然后由△ACO和△ACB的面积和等于△AOB的面积求出CF,在直角三角形BFC中,由三角函数求出BC,从而求出OC.
解答 解:∵A(1,$\sqrt{3}$),B(4,0),
∴OA=$\sqrt{(1-0)^{2}+(\sqrt{3}-0)^{2}}$=2,
AB=$\sqrt{(4-0)^{2}+(\sqrt{3}-0)^{2}}$=2$\sqrt{3}$,
OB=4,
22+(2$\sqrt{3}$)2=42,即:OA2+AB2=OB2,
∴△AOB为直角三角形,∠OAB=90°,
又∵OA=2,OB=4,
∴∠ABO=30°,
过点D作AO和AB的垂线分别交AO和AB于E、F, ∵∠OAB的平分线AC,
∵∠OAB的平分线AC,
∴CE=CF,
△ACO和△ACB的面积和等于△AOB的面积,
则:$\frac{1}{2}$OA•CE+$\frac{1}{2}$AB•CF=$\frac{1}{2}$OA•AB,
∴CF+$\sqrt{3}$CF=2$\sqrt{3}$,
解得:CF=3-$\sqrt{3}$,
在直角三角形BFC中,
BC=$\frac{CF}{sin30°}$=$\frac{3-\sqrt{3}}{\frac{1}{2}}$=6-2 $\sqrt{3}$,
∴OC=OB-BC=4-(6-2 $\sqrt{3}$)=2 $\sqrt{3}$-2.
点评 此题考查的知识点是解直角三角形,关键是运用两点间的距离公式通过计算得出△AOB为直角三角形且∠ABO=30°,再运用三角形面积求出CF,利用直角三角形三角函数求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,直线l1:y=-x+6与x轴交于点B,与直线l2:y=$\frac{1}{2}$x交与点A,点E为线段OA的中点,点F为线段CD的中点,长为2的动线段CD(端点C从原点O开始)在线段OB上以每秒1个单位的速度向点B运动,当端点D到达点B时运动停止.设运动时间为t秒,那么当t=$\frac{7}{3}$秒时,四边形AECF的周长最小.
如图,直线l1:y=-x+6与x轴交于点B,与直线l2:y=$\frac{1}{2}$x交与点A,点E为线段OA的中点,点F为线段CD的中点,长为2的动线段CD(端点C从原点O开始)在线段OB上以每秒1个单位的速度向点B运动,当端点D到达点B时运动停止.设运动时间为t秒,那么当t=$\frac{7}{3}$秒时,四边形AECF的周长最小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一筒状的地膜示意图,其内圆半径和外圆半径分别为r=10厘米和R=20厘米,高h=50厘米.如果地膜的厚度是0.005厘米,你能计算出这些地膜的总长度是多少吗?
如图是一筒状的地膜示意图,其内圆半径和外圆半径分别为r=10厘米和R=20厘米,高h=50厘米.如果地膜的厚度是0.005厘米,你能计算出这些地膜的总长度是多少吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 只有一解x=2 | B. | 任意实数都是解 | C. | 无解 | D. | 解为x≠2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com