
ЁОЬтФПЁПФГаЃОХФъМЖЃЈ1ЃЉАрЫљгабЇЩњВЮМг2016ФъГѕжаБЯвЕЩњЩ§бЇЬхг§ВтЪдЃЌИљОнВтЪдЦРЗжБъзМЃЌНЋЫћУЧЕФГЩМЈНјааЭГМЦКѓЗжЮЊAЁЂBЁЂCЁЂDЫФЕШЃЌВЂЛцжЦГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЈЮДЭъГЩЃЉЃЌЧыНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
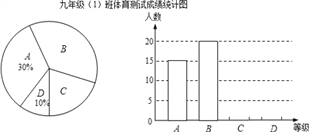
ЃЈ1ЃЉЁЂОХФъМЖЃЈ1ЃЉАрВЮМгЬхг§ВтЪдЕФбЇЩњга ШЫЃЛ
ЃЈ2ЃЉЁЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећ.
ЃЈ3ЃЉЁЂдкЩШаЮЭГМЦЭМжаЃЌЕШМЖBВПЗжЫљеМЕФАйЗжБШЪЧ ЃЛ
ЃЈ4ЃЉЁЂШєИУаЃОХФъМЖбЇЩњЙВга850ШЫВЮМгЬхг§ВтЪдЃЌЙРМЦДяЕНAМЖКЭBМЖЕФбЇЩњЙВгаЖрЩйШЫЃП
ЁОД№АИЁПЃЈ1ЃЉ50ЃЛЃЈ2ЃЉВЙЭММћНтЮіЃЛЃЈ3ЃЉ72ЖШЃЛЃЈ4ЃЉЙРМЦДяЕНAМЖКЭBМЖЕФбЇЩњЙВга595ШЫ.
ЁОНтЮіЁПЃЈ1ЃЉгЩAЕШЕФШЫЪ§КЭБШР§ЃЌИљОнзмЪ§=ФГЕШШЫЪ§ЁТЫљеМЕФБШР§МЦЫуЃЛ
ЃЈ2ЃЉИљОнЁАзмЪ§=ФГЕШШЫЪ§ЁТЫљеМЕФБШР§ЁБМЦЫуГіDЕШЕФШЫЪ§ЃЌзмЪ§-ЦфЫќЕШЕФШЫЪ§=CЕШЕФШЫЪ§ЃЛ
ЃЈ3ЃЉгЩзмЪ§=ФГЕШШЫЪ§ЁТЫљеМЕФБШР§МЦЫуГіBЕШЕФБШР§ЃЌгЩзмБШР§ЮЊ1МЦЫуГіCЕШЕФБШР§ЃЌЖдгІЕФдВаФНЧ=360ЁуЁСБШР§ЃЌЮЪЬтЕУНтЃЎ
ЃЈ4ЃЉИљОнAЁЂBдкбљБОжаЕФБШР§МДПЩЙРЫуГіНсЙћ.
НтЃКЃЈ1ЃЉзмШЫЪ§=AЕШШЫЪ§ЁТAЕШЕФБШР§=15ЁТ30%=50ШЫ
ЙЪД№АИЮЊ50ЃЛ
ЃЈ2ЃЉDЕШЕФШЫЪ§=змШЫЪ§ЁСDЕШБШР§=50ЁС10%=5ШЫЃЌCЕШШЫЪ§=5020155=10ШЫЃЌ
ШчЭМЫљЪОЃЛ
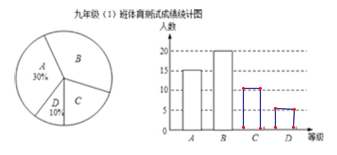
ЃЈ3ЃЉBЕШЕФБШР§=20ЁТ50=40%ЃЌ
CЕШЕФБШР§=140%10%30%=20%ЃЌ
CЕШЕФдВаФНЧ=360ЁС20%=72Ёу.
ЙЪД№АИЮЊЃК72Ёу.
ЃЈ4ЃЉ![]() ЃЈШЫЃЉ.
ЃЈШЫЃЉ.
Д№ЃКЙРМЦДяЕНAМЖКЭBМЖЕФбЇЩњЙВга595ШЫ.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЄУїЬт
ЃЈ1ЃЉвбжЊвЛдЊЖўДЮЗНГЬx2+px+q=0ЃЈp2-4qЁн0ЃЉЕФСНИљЮЊx1ЁЂx2ЃЛЧѓжЄЃКx1+x2=-p ЃЌ x1 x2=q ЃЎ
ЃЈ2ЃЉвбжЊХзЮяЯпy=x2+px+qгыxжсНЛгкAЁЂBСНЕуЃЌЧвЙ§ЕуЃЈ-1ЃЌ-1ЃЉЃЌЩшЯпЖЮABЕФГЄЮЊdЃЌЕБpЮЊКЮжЕЪБЃЌd2ШЁЕУзюаЁжЕЃЌВЂЧѓГізюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖдГЦжсЮЊжБЯпx=2ЕФХзЮяЯпy=x2+bx+cгыxжсНЛгкЕуAКЭЕуBЃЌгыyжсНЛгкЕуCЃЌЧвЕуAЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉ
зЂЃКЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЖЅЕузјБъЮЊЃЈЉ ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБНгаДГіBЁЂCСНЕуЕФзјБъЃЛ
ЃЈ3ЃЉЧѓЙ§OЃЌBЃЌCШ§ЕуЕФдВЕФУцЛ§ЃЎЃЈНсЙћгУКЌІаЕФДњЪ§ЪНБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌMNЪЧЁбOЕФжБОЖЃЌMN=4ЃЌЁЯAMN=40ЁуЃЌЕуBЮЊЛЁANЕФжаЕуЃЌЕуPЪЧжБОЖMNЩЯЕФвЛИіЖЏЕуЃЌдђPA+PBЕФзюаЁжЕЮЊ ЃЎ 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЭМаЮжаЃЌМШЪЧжсЖдГЦЭМаЮгжЪЧжааФЖдГЦЭМаЮЕФЪЧЃЈЁЁЁЁЃЉ
A.
B.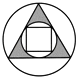
C.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїABCжаЃЌЁЯBAD=ЁЯEBCЃЌADНЛBEгкF.
(1)ЪдЫЕУї : ЁЯABC=ЁЯBFD ЃЛ
(2)ШєЁЯABC=35ЁуЃЌEGЁЮADЃЌEHЁЭBEЃЌЧѓЁЯHEGЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкВЛЕШЪНзщ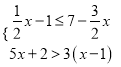 ЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. ДЫВЛЕШЪНзщЮоНт B. ДЫВЛЕШЪНзщга7ИіећЪ§Нт
C. ДЫВЛЕШЪНзщЕФИКећЪ§НтЪЧЉ3ЃЌЉ2ЃЌЉ1 D. ДЫВЛЕШЪНзщЕФНтМЏЪЧ![]() ЃМxЁм2
ЃМxЁм2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГАргабЇЩњ55ШЫЃЌЦфжаФаЩњгыХЎЩњЕФШЫЪ§жЎБШЮЊ6ЃК5ЁЃ
ЃЈ1ЃЉЧѓГіИУАрФаЩњгыХЎЩњЕФШЫЪ§ЃЛ
ЃЈ2ЃЉбЇаЃвЊДгИУАрбЁГі20ШЫВЮМгбЇаЃЕФКЯГЊЭХЃЌвЊЧѓЃКЂйФаЩњШЫЪ§ВЛЩйгк7ШЫЃЛЂкХЎЩњШЫЪ§ГЌЙ§ФаЩњШЫ
Ъ§2ШЫвдЩЯЁЃЧыЮЪФаЁЂХЎЩњШЫЪ§гаМИжжбЁдёЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫУРЛЏаЃдАЛЗОГЃЌељДДТЬЩЋбЇаЃЃЌФГЯиНЬг§ОжЮЏЭадАСжЙЋЫОЖдAЃЌBСНаЃНјаааЃдАТЬЛЏЃЌвбжЊAаЃгаШчЭМ![]() ЕФвѕгАВПЗжПеЕиашЦЬЩшВнЦКЃЌBаЃгаШчЭМ
ЕФвѕгАВПЗжПеЕиашЦЬЩшВнЦКЃЌBаЃгаШчЭМ![]() ЕФвѕгАВПЗжПеЕиашЦЬЩшВнЦКЃЌдкМзЁЂввСНЕиЗжБ№гаЭЌжжВнЦЄ3500Уз
ЕФвѕгАВПЗжПеЕиашЦЬЩшВнЦКЃЌдкМзЁЂввСНЕиЗжБ№гаЭЌжжВнЦЄ3500Уз![]() КЭ2500Уз
КЭ2500Уз![]() ГіЪлЃЌЧвЪлМлвЛбљЃЌШєдАСжЙЋЫОЯђМзЁЂввСНЕиЙКТђВнЦЄЃЌЦфТЗГЬКЭдЫЗбЕЅМлБэШчЯТЃК
ГіЪлЃЌЧвЪлМлвЛбљЃЌШєдАСжЙЋЫОЯђМзЁЂввСНЕиЙКТђВнЦЄЃЌЦфТЗГЬКЭдЫЗбЕЅМлБэШчЯТЃК
ТЗГЬЁЂдЫЗбЕЅМлБэ
AаЃ | BаЃ | |||
ТЗГЬ | дЫЗбЕЅМл | ТЗГЬ | дЫЗбЕЅМл | |
МзЕи | 20 |
| 10 |
|
ввЕи | 15 |
| 20 | |
![]() зЂЃКдЫЗбЕЅМлБэЪОУПЦНЗНУзВнЦЄдЫЫЭ1ЧЇУзЫљашЕФШЫУёБв
зЂЃКдЫЗбЕЅМлБэЪОУПЦНЗНУзВнЦЄдЫЫЭ1ЧЇУзЫљашЕФШЫУёБв![]()

ЧѓЃК![]() ЗжБ№ЧѓГіЭМ1ЁЂЭМ2ЕФвѕгАВПЗжУцЛ§ЃЛ
ЗжБ№ЧѓГіЭМ1ЁЂЭМ2ЕФвѕгАВПЗжУцЛ§ЃЛ
![]() ШєдАСжЙЋЫОНЋМзЕи
ШєдАСжЙЋЫОНЋМзЕи![]() ЕФВнЦЄШЋВПдЫЭљAаЃЃЌЧыФуЧѓГідАСжЙЋЫОдЫЫЭВнЦЄШЅAЁЂBСНаЃЕФзмдЫЗбЃЛ
ЕФВнЦЄШЋВПдЫЭљAаЃЃЌЧыФуЧѓГідАСжЙЋЫОдЫЫЭВнЦЄШЅAЁЂBСНаЃЕФзмдЫЗбЃЛ
![]() ЧыФуИјГівЛжждЫЫЭЗНАИЃЌЪЙЕУдАСжЙЋЫОжЇИЖГіЫЭВнЦЄЕФзмдЫЗбВЛГЌЙ§15000дЊЃЎ
ЧыФуИјГівЛжждЫЫЭЗНАИЃЌЪЙЕУдАСжЙЋЫОжЇИЖГіЫЭВнЦЄЕФзмдЫЗбВЛГЌЙ§15000дЊЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com