
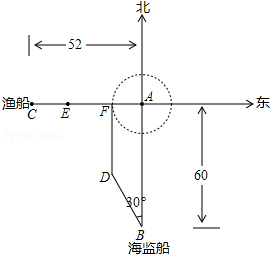
 ���㵺�������й�����������ΪԲ������Χ12���ﷶΧ�ھ����ڽ�����������������ֻ���룬��ͼ������һ�й����ബ��λ�ڵ� �㵺A���Ϸ��ൺ60�����B������Ѳ�ߣ�ֵ����Ա�����ڵ��㵺����������52�����C����һ���ձ��洬������9�ڵ��ٶ�����������ʻ����㵺���з��������ձ��洬�������棬���ر�ƫ��30��ķ�����12�ڵ��ٶ�ǰ�����أ��ڼ��η������棬2Сʱ�ബ����D�������ͬʱ�ձ��洬����E������ʱ���ബ�ٴη������ؾ��森
���㵺�������й�����������ΪԲ������Χ12���ﷶΧ�ھ����ڽ�����������������ֻ���룬��ͼ������һ�й����ബ��λ�ڵ� �㵺A���Ϸ��ൺ60�����B������Ѳ�ߣ�ֵ����Ա�����ڵ��㵺����������52�����C����һ���ձ��洬������9�ڵ��ٶ�����������ʻ����㵺���з��������ձ��洬�������棬���ر�ƫ��30��ķ�����12�ڵ��ٶ�ǰ�����أ��ڼ��η������棬2Сʱ�ബ����D�������ͬʱ�ձ��洬����E������ʱ���ബ�ٴη������ؾ��森���� ��1������E��ԲA������EN�������AEN�Ķ������ɵó��𰸣�
��2���ֱ�����洬�����ബ�����F��ʱ�䣬Ȼ��ȽϿ������жϣ�
���  �⣺��1������E��ԲA������EN������AN����AN��EN��
�⣺��1������E��ԲA������EN������AN����AN��EN��
������ã�CE=9��2=18�����AE=AC-CE=52-18=34���
��sin��AEN=$\frac{AN}{AE}$=$\frac{12}{34}$��0.35��
���AEN=20.5�㣬
���NEM=69.5�㣬
�������ر�ƫ������ת��69.5�㺽�У�����ǡ�ñ��������㵺12���������
��2������D��DH��AB�ڵ�H��
������ã�BD=2��12=24���
��Rt��DBH��DH=$\frac{1}{2}$BD=12���BH=12$\sqrt{3}$���
��AF=12���
��DH=AF��
��DF��AF��
��ʱ���ബ���������ʻ��
���ബ�����F��ʱ��Ϊ��$\frac{DF}{18}$=$\frac{AB-BH}{18}$=$\frac{60-12\sqrt{3}}{18}$��2.2Сʱ��
�洬�����F��ʱ��Ϊ��$\frac{EF}{9}$=$\frac{52-18-12}{9}$��2.4Сʱ��
��2.2��2.4��
�ຣ�ബ���ձ��洬�ȵ���F����
���� ���⿼���˽�ֱ�������ε�Ӧ�ã������Ĺؼ��ǹ���ֱ�������Σ���������ʱ��������⣬������ӱ����һ���ܺõ���Ŀ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
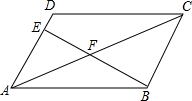 ��ͼ����ƽ���ı���ABCD�У�AE��AD=2��3������BE��AC�ڵ�F������ABF���ı���CDEF������ֱ��ΪS1��S2����S1��S2Ϊ��������
��ͼ����ƽ���ı���ABCD�У�AE��AD=2��3������BE��AC�ڵ�F������ABF���ı���CDEF������ֱ��ΪS1��S2����S1��S2Ϊ��������| A�� | 2��3 | B�� | 4��9 | C�� | 6��11 | D�� | 6��13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 12 | C�� | 5 | D�� | 3.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1-x-3=3x | B�� | 6-2x-6=3x | C�� | 6-x+3=3x | D�� | 1-x+3=3x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABΪ��0��ֱ����$\widehat{BC}$=$\widehat{CD}$��CE��AD��E��OE��AC�ڵ�F��
��ͼ��ABΪ��0��ֱ����$\widehat{BC}$=$\widehat{CD}$��CE��AD��E��OE��AC�ڵ�F���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com