
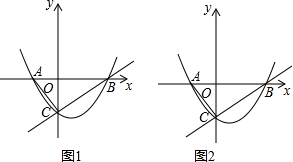
���� ��1������ֱ��BC�Ľ���ʽ����ȷ��B��C�����꣬���������ߵĽ���ʽ�У�����ȷ������ϵ����ֵ��
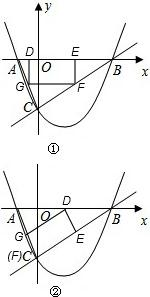
��2���پ���������������AB���ϣ���������ΪD��E�����������DG�ij�Ϊm���������������Ρ�CFG�ס�CBA�õ��ı����߶Σ������GF�ı���ʽ�������ɸ��ݾ��ε������ʽ������ھ��ε������m�ĺ�����ϵʽ�����ݺ��������ʼ��ɵõ����ε�����������Ӧ��mֵ���Ӷ�ȷ�������ε��Ķ�������ꣻ
�ھ�����һ��������AB���ϣ���ΪD������ʱC��F�غϣ�����ͬ�٣�������DE=n���ɡ�ADG�ס�ABC���DG�ij����������ݾ��ε������ʽ�õ����ھ��ε������n�ĺ�����ϵʽ���Ӷ����ݺ�����������þ��ε��������Ͷ�Ӧ��nֵ������ȷ�����ε��ĸ��������꣮
��3���ֵ�P�ڵ�A��������ұ�������������ݵ�P�������ʾ��AP�ij��������á�OBC������ֵ��ʾ��PM��������ԳƵ����ʱ�ʾ��PQ�����á�QPH�����ұ�ʾ��QH�����ұ�ʾ��PH���Ӷ����Ա�ʾ��OH���ٸ������߶�Ӧ�ɱ������н���ȣ������������ƣ������������ʽ��⼴�ɣ�
���  �⣺��1��ֱ��y=$\frac{1}{2}$x-2�У���y=0����x=4����x=0����y=-2��
�⣺��1��ֱ��y=$\frac{1}{2}$x-2�У���y=0����x=4����x=0����y=-2��
��B��4��0����C��0��-2����
���������߾�����C��0��-2������c=-2��
��B���������y=$\frac{1}{2}$x2-bx-2�У��ã�b=-$\frac{3}{2}$��
�������ߵĽ���ʽΪy=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
��2�����ݣ�1���еĺ�������ʽ��֪A��-1��0����B��4��0����C��0��-2����
��AB=5��AC=$\sqrt{5}$��BC=2$\sqrt{5}$��
��AC2+BC2=5+20=25=AB2��
���ABC��ֱ�������Σ��ҡ�ACB=90�㣮
������������ۣ�
����ͼ1��ʾ������DEFG��D��E��AB���ϣ�
��DG=EF=m��
����FG��x�ᣬ���CGF�ס�CAB��
$\frac{2-m}{2}$=$\frac{FG}{5}$��
��ã�FG=5-$\frac{5}{2}$m��
����ε����S=DG•FG=��5-$\frac{5}{2}$m��m=-$\frac{5}{2}$m2+5m��
��S=-$\frac{5}{2}$��m-1��2+$\frac{5}{2}$��
��m=1ʱ�����ε�������Ϊ2.5��
��ʱD��-$\frac{1}{2}$��0����E��2��0����G��-$\frac{1}{2}$��-1����F��2��-1����
����ͼ2��ʾ������DEFG�У�F��C�غϣ�D��AB���ϣ�
��DE=CG=n��ͬ�ٿɵã���DG=2$\sqrt{5}$-2n��
����ε����S=DE•DG=��2$\sqrt{5}$-2n��n=-2��n-$\frac{\sqrt{5}}{2}$��2+$\frac{5}{2}$��
����n=$\frac{\sqrt{5}}{2}$ʱ�����ε�������Ϊ2.5��
OD=OB-BD=$\sqrt{5}$��
��D��$\sqrt{5}$��0�����������������ε�������Ϊ2.5����ʱ������AB���ϵĶ�������Ϊ��-$\sqrt{5}$��0������2�� 0����$\sqrt{5}$��0����
0����$\sqrt{5}$��0����
��3�����ݣ�1���еĺ�������ʽ��֪B��4��0����C��0��-2������OB=4��OC=2��BC=2$\sqrt{5}$��
����ͼ�ۣ�����P�ڵ�A���ұ�ʱ��
�ߵ�P������Ϊ��t��0����
��BP=4-t��PM=BP•sin��OBC=��4-t��•$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$��4-t����
��P��Q�������ֱ��BC��Գƣ�PQ��BC�ڵ�M��
��PQ=2PM=$\frac{2\sqrt{5}}{5}$��4-t����
QH=PQ•sin��QPH=PQ•cos��OBC=$\frac{2\sqrt{5}}{5}$��4-t����$\frac{4}{2\sqrt{5}}$=$\frac{4}{5}$��4-t����
PH=PQ•cos��QPH=PQ•sin��OBC=$\frac{2\sqrt{5}}{5}$��4-t����$\frac{2}{2\sqrt{5}}$=$\frac{2}{5}$��4-t����
����P��ԭ����Ҳ�ʱ��OH=OP+PH=t+$\frac{2}{5}$��4-t��=$\frac{3t}{5}$+$\frac{8}{5}$��
�ߡ�PQH���APM���ƣ�
��tan��OAB=tan��PQH��
���t=-16����ȥ������t=8��
�ڵ���P�ڵ�A�����ʱ��
�ߵ�P������Ϊ��t��0����
��AP=4-t��PM=AP•sin��OAB=��4-t����
��P��Q�������ֱ��AB��Գƣ�PQ��AB�ڵ�M��
��PQ=2PM=��4-t����
QH=PQ•sin��QPH��
PH=PQ•cos��QPH��
����P�ڵ�O�Ҳ�ʱ��OH=OP+PH��
�ߡ�OQH���APM���ƣ�
��tan��OAB=tan��OAB��
����P�ڵ�O���ʱ��OH=OP-PH��
�ߡ�OQH���APM���ƣ�
��tan��OAB=tan��OAB��
���t=-16��t=8����ȥ��
��������������t��ֵ��t=0��t=��t=-16��t=8��ʹ��OQH���APM���ƣ�
���� �����ǶԶ��κ������ۺϿ��飬��Ҫ�漰���κ�����������Ľ��㣬��������κ��������������ζ�Ӧ�߳ɱ�������ֱ�������Σ���3��Ҫ�ֵ�P�ڵ�A��������������������ۣ����ݵ�P��λ�õIJ�ͬ���ֱ��г�OH�IJ�ͬ��ʾ�ǽ���Ĺؼ�����Ҫ�������������ζ�Ӧ�߲���ȷ��Ҫ��������ۣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com