
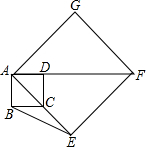
 如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )
如图,正方形ABCD的顶点C在正方形AEFG的边AE上,AB=2,AE=4$\sqrt{2}$,则点G到BE的距离( )| A. | $\frac{32\sqrt{2}}{5}$ | B. | $\frac{36\sqrt{2}}{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | $\frac{18\sqrt{5}}{5}$ |
分析 根据平行线的判定,可得AB与GE的关系,根据平行线间的距离相等,可得△BEG与△AEG的关系,根据根据勾股定理,可得AH与BE的关系,再根据勾股定理,可得BE的长,根据三角形的面积公式,可得G到BE的距离.
解答 解:连接GB、GE,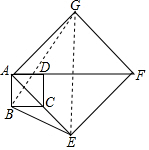
由已知α=45°,可知∠BAE=45°.
又∵GE为正方形AEFG的对角线,
∴∠AEG=45°.
∴AB∥GE.
∵AE=4$\sqrt{2}$,AB与GE间的距离相等,
∴GE=8,${S}_{△BEG}={S}_{△AEG}=\frac{1}{2}{S}_{AEFG}=16$.
过点B作BH⊥AE于点H,
∵AB=2,
∴$BH=AH=\sqrt{2}$.
∴$HE=3\sqrt{2}$.
∴$BE=2\sqrt{5}$.
设点G到BE的距离为h.
∴${S}_{△BEG}=\frac{1}{2}•BE•h=\frac{1}{2}×2\sqrt{5}×h=16$.
∴$h=\frac{16\sqrt{5}}{5}$.
即点G到BE的距离为$\frac{16\sqrt{5}}{5}$.
故选C
点评 本题主要考查了几何变换综合题.涉及正方形的性质,全等三角形的判定及性质,等积式及四点共圆周的知识,综合性强.解题的关键是运用等积式及四点共圆的判定及性质求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF
如图,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试说明:CD∥EF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
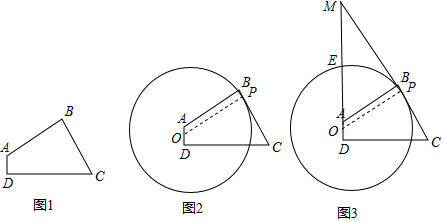
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com