
【题目】如图,点A、B、C、D在一条直线上,AB=CD,四边形BECF是平行四边形. 
(1)求证:△AEC≌△DFB;
(2)求证:∠AEB=∠DFC.
【答案】
(1)证明:∵四边形BECF是平行四边形.
∴CE=BF,BE∥CF,BE=CF,
∴∠ACE=∠DBF,
∵AB=CD,
∴AC=DB,
在△AEC和△DFB中,  ,
,
∴△AEC≌△DFB(SAS);
(2)证明:∵△AEC≌△DFB,
∴AE=DF,
在△AEB和△DFC中,  ,
,
∴△AEB≌△DFC(SSS),
∴∠AEB=∠DFC.
【解析】(1)由SAS证明△AEC≌△DFB即可;(2)由由SSS证明△AEB≌△DFC,即可得出结论.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在AC⊥BC,过点C的直线MN∥AB,D为AB边上一点,且AD=4,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求CE的长;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:新京报讯 (记者沙璐摄影彭子洋)5月7日,第五届北京农业嘉年华圆满闭幕.历时58天的会期,共接待游客136.9万人次,累计实现总收入3.41亿元.其中4月3日的接待量为10.6万人次,创下了五届农业嘉年华以来单日游客人数的最高纪录.
本届北京农业嘉年华共打造了180余个创意景观,汇集了680余个农业优新特品种、130余项先进农业技术,开展了210余项娱乐游艺和互动体验活动. 在去年“三馆两园一带一谷”的基础上,增设了“一线”,即京北旅游黄金线,并在草莓博览园作为主会场的同时,首设乐多港、延寿两大分会场.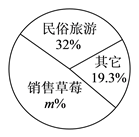
据统计,本届嘉年华期间共有600余家展商参展,设置了1700处科普展板,近6万人参与“草莓票香”体验活动,周边各草莓采摘园接待游客达267万人次,销售草莓265.6万公斤,实现收入1.659亿元.同时,还有效带动延寿、兴寿、小汤山、崔村、百善、南邵6个镇的民俗旅游,实现收入1.09亿元,较上届增长14.84%.
根据以上材料回答下列问题:
(1)举办农业嘉年华以来单日游客人数的最高纪录是;
(2)如右图,用扇形统计图表示民俗旅游、销售草莓及其它方面收入的分布情况,则m=;
(3)选择统计表或统计图,将本届嘉年华的创意景观、农业优新特品种、展商参展、科普展板的数量表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 . 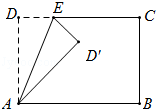
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作…若在第 n 次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.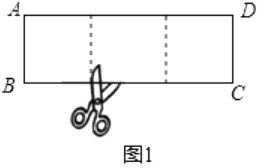
(1)判断与操作:
如图2,矩形ABCD的长为5,宽为2,它是奇异矩形吗?
如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.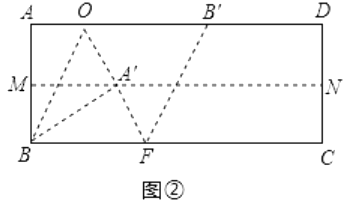
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;以此进行下去…,则正方形AnBnCnDn的面积为( ) 
A.( ![]() )n
)n
B.5n
C.5n﹣1
D.5n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(2)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com