
【题目】(1)如图1,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG,BF⊥AG,垂足分别为点E,F.求证:![]() ;
;

(2)在图1的基础上,若过点C作CH⊥DE,垂足为点H,连接AH,CF,如图2.求证:四边形AFCH为平行四边形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据正方形的性质及已知条件证明△ADE≌△BAF,得到DE=AF ,再利用在Rt△ABF中![]() ,得到
,得到![]() ;
;
(2)同理可证△ADE≌△DCH(AAS)得到DE=CH故得到CH=AF,再根据CH⊥DE,DE⊥AG
得到CH∥AF故可证明四边形AFCH为平行四边形.
(1)证明:∵四边形ABCD是正方形
∴AB=DA,∠BAD=90°
∴∠BAF+∠DAE=90°
∵DE⊥AG,BF⊥AG
∴∠AED=∠BFA=90°
∴∠BAF+∠ABF=90°
∴∠DAE=∠ABF
在△ADE与△BAF中

∴△ADE≌△BAF(AAS)
∴DE=AF
在Rt△ABF中
∵![]()
∴![]()
(2)同理可得:△ADE≌△DCH(AAS)…
∴DE=CH
又∵由(1)可得:DE=AF
∴CH=AF
∵CH⊥DE,DE⊥AG
∴∠CHE=∠AED=90°
∴CH∥AF
∴四边形AFCH为平行四边形


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,AC∥BD,请先作图再解决问题.
(1)利用尺规完成以下作图,并保留作图痕迹.(不要求写作法)
①作BE平分∠ABD交AC于点E;
②在BA的延长线上截取AF=BA,连接EF;
(2)判断△BEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
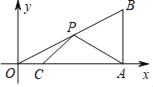
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建造一个四边形花圃ABCD,要求AD边靠墙,CD⊥AD,AD∥BC,AB∶CD=5∶4,且三边的总长为20 m.设AB的长为5x m.
(1)请求AD的长;(用含字母x的式子表示)
(2)若该花圃的面积为50 m2,且周长不大于30 m,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知∠B=∠BGD,∠DGF=∠F,求证:∠B+∠F=180°.
请你认真完成下面的填空.
证明:∵∠B=∠BGD ( 已知 )
∴AB∥CD ( )
∵∠DGF=∠F;( 已知 )
∴CD∥EF ( )
∴AB∥EF ( )
∴∠B+∠F=180°( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小英与她的父亲,母亲计划外出旅游,初步选择了延安、西安、汉中、安康四个城市,由于时间仓促,他们只能去其中一个城市,到底去哪一个城市三人意见不统一,在这种情况下,小英父亲建议,用小英学过的摸球游戏来决定,规则如下:
①在一个不透明的袋子中装一个红球(延安)、一个白球(西安)、一个黄球(汉中)和一个黑球(安康),这四个球除颜色的不同外,其余完全相同;
②小英父亲先将袋中球摇匀,让小英从袋中随机摸出一球,父亲记录下其颜色,并将这个球放回袋中摇匀;然后让小英母亲从袋中随机摸出一球,父亲记录下它的颜色;
③若两人所摸出球的颜色相同,则去该球所表示的城市旅游。否则,前面的记录作废,按规则②重新摸球,直到两人所摸出的球的颜色相同为止。
按照上面的规则,请你解答下列问题:
(1)已知小英的理想旅游城市是西安,小英和母亲随机各摸球一次,均摸出白球的概率是多少?
(2)已知小英母亲的理想旅游城市是汉中,小英和母亲随机各摸球一次,至少有一人摸出黄球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 AD//BC, 点 E 为 CD 上一点,AE、BE 分别平分∠DAB、∠CBA,BE交 AD 的延长线于点 F.求证:(1)△ABE≌△AEF;(2) AD+BC=AB

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB⊥AC,AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A,E两点.
(1)如图2,当⊙P与边CD相切于点F时,求AP的长;
(2)不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com