
【题目】今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
到社区供水点的路程(千米) | 运费(元/吨·千米) | |
甲厂 | 20 | 12 |
乙厂 | 14 | 15 |
【1】若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
【2】设从甲厂调运饮用水![]() 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
【答案】
【1】 设从甲厂调运了x吨饮用水,从乙厂调运了y吨饮用水,
由题意得:![]() ,
,
解得:![]() ,
,
∵50≤80,70≤90,
∴符合条件,
∴从甲、乙两水厂各调运了50吨、70吨饮用水;(4分)
【2】 从甲厂调运饮用水x吨,则需从乙调运水120-x吨,
∵x≤80,且120-x≤90,
∴30≤x≤80,
总运费W=20×12x+14×15(120-x)=30x+25200,
∵W随X的增大而增大,
∴当x=30时,W最小=26100元,
∴每天从甲厂调运30吨,从乙厂调运90吨,每天的总运费最省.(5分)
【解析】
试题(1)设从甲厂调运饮用水x吨,从乙厂调运饮用水y吨,根据“每天需从社区外调运饮用水120吨,调运水的总运费为26700元”即可列方程组求解;
(2)设从甲厂调运饮用水x吨,则需从乙厂调运水(120-x)吨,根据“甲厂每天最多可调出80吨,乙厂每天最多可调出90吨”即可列不等式组求得x的范围,再根据题意列出![]() 关于
关于![]() 的函数关系式,最后根据一次函数的性质求解即可.
的函数关系式,最后根据一次函数的性质求解即可.
(1)设从甲厂调运饮用水x吨,从乙厂调运饮用水y吨,根据题意得
![]() 解得
解得![]()
∵50![]() 80,70
80,70![]() 90,∴符合条件
90,∴符合条件
故从甲、乙两水厂各调用了50吨、70吨饮用水;
(2)设从甲厂调运饮用水x吨,则需从乙厂调运水(120-x)吨,根据题意可得
![]() 解得
解得![]() .
.
总运费![]() ,(
,(![]() )
)
∵W随x的增大而增大,故当![]() 时,
时,![]() 元.
元.
∴每天从甲厂调运30吨,从乙厂调运90吨,每天的总运费最省,最少为26100元.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)点D是抛物线上的一动点,是否存在点D,使得tan∠DCB=tan∠ACO.若存在,请求出点D的坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
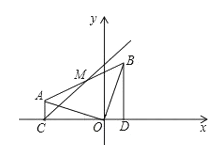
【题目】在平面直角坐标系中有一△BOD,![]() ,把 BO 绕点O 逆时针旋转 90°得OA, 连接AB,作
,把 BO 绕点O 逆时针旋转 90°得OA, 连接AB,作![]() 于点 C,点B 的坐标为(1,3).
于点 C,点B 的坐标为(1,3).
(1)求直线AB 的解析式;
(2)若AB 中点为 M,连接 CM,动点 P、Q 同时从 C 点出发,点 P 沿射线CM 以每秒2个单位长度的速度运动,点Q沿线段CD 以每秒1个单位长度的速度向终点 D 运动,当Q点运动到D 点时,P、Q同时停止运动,设△PQO 的面积为 S(![]() ),运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围;
),运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,是否存在这样的 P 点,使得P、O、B为顶点的三角形是直角三角形?若存在,求出对应的t 值和此时Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,过原点O及点A(0,4)、C(12,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒2![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒4个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒4个单位长度的速度沿x轴正方向移动.设移动时间为t秒.

(1)当点P移动到点D时,求出此时t的值.
(2)当t为何值时,△PQB为直角三角形.
(3)已知过O、P、Q三点的抛物线解析式为y=﹣![]() .问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
.问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放假时小华父子俩一同出发去露营,步行途中小华发现睡袋忘拿了跑步回家取,之后立刻返程跑步追赶爸爸,期间爸爸继续步行去往露营地,会合时爸爸发现还需要探照灯,为节约时间爸爸乘车回家去拿,小华继续步行至露营地,爸爸拿到探照灯后乘车也到了终点(假定步行、跑步和汽车均为匀速,且二人取物品时间忽略不计),二人之间的距离s(米)与他们出发时间t(分钟)之间的关系如图所示,则当爸爸到家时,小华与露营地相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 上的两动点,
上的两动点,![]() 从点
从点![]() 开始以
开始以![]() 的速度向点
的速度向点![]() 运动,
运动,![]() 从点
从点![]() 开始以
开始以![]() 的速度向点
的速度向点![]() 运动,当一点到达终点时,
运动,当一点到达终点时,![]() 、
、![]() 两点就同时停止运动.设运动时间为
两点就同时停止运动.设运动时间为![]() .
.

(1)用![]() 的代数式分别表示
的代数式分别表示![]() 和
和![]() 的长;
的长;
(2)设![]() 的面积为
的面积为![]() ,
,
①求![]() 的面积
的面积![]() 与
与![]() 的关系式;
的关系式;
②当![]() 时,
时,![]() 的面积
的面积![]() 是多少?
是多少?
(3)当![]() 为多少秒时,以点
为多少秒时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:下列图案是山西晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,随着基本图案的增加所贴剪纸“○”的总个数也在发生变化.

(1)填写下表:
第 | 1 | 2 | 3 | 4 | …… |
“○”的总个数 | …… |
(2)请你写出第![]() 个图案中“○”的总个数
个图案中“○”的总个数![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?请补全频数分布直方图;
(2)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(3)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com