

分析 首先证明△OBD是等边三角形,再证明AB=AC,∠ACB=∠D=60°即可解决问题.
(2)如图2中,连接CD,作PN⊥CD交CD的延长线于N,PF⊥AD于F,PE⊥BC于E.首先证明,PN=PF,PN=PE,推出PE=PF,推出∠PKE=∠PKF即可解决问题.
(3)如图3中,连接CD,作DF⊥CM于F,PE⊥BC于E.只要证明△PDF是等腰直角三角形,求出PD即可解决问题.
解答 (1)证明:如图1中,连接OB.
∵弦BC垂直平分半径OD,
∴BK=CK,BO=BD=OD,
∴AB=AC,△OBD是等边三角形,
∴∠ACB=∠D=∠ABC=60°,
∴△ABC是等边三角形.
(2)如图2中,连接CD,作PN⊥CD交CD的延长线于N,PF⊥AD于F,PE⊥BC于E.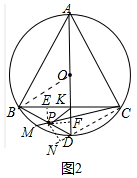
由(1)可知,∠BAC=∠ADB=60°,
∵∠BDC+∠BAC=180°,
∴∠BDC=120°,
∴∠BDN=∠BDA,
∴PN=PF,
∵$\widehat{BM}$=$\widehat{MD}$,
∴∠MCB=∠MCD,
∴PE=PN,
∴PE=PF,∵PF⊥AD于F,PE⊥BC于E,
∴∠PKE=∠PKF,∵∠BKD=90°,
∴∠BKP=45°,
∴sin∠BKP=$\frac{\sqrt{2}}{2}$.
(3)如图3中,连接CD,作DF⊥CM于F,PE⊥BC于E.
在Rt△PEK中,∵∠PKE=45°,PK=2$\sqrt{3}$,
∴EK=PE=$\frac{\sqrt{2}}{2}$•PK=$\sqrt{6}$,
在Rt△BEK中,∵∠PBE=30°,PE=$\sqrt{6}$,
∴BE=$\sqrt{3}$PE=3$\sqrt{2}$,BP=2PE=2$\sqrt{6}$,
在Rt△BDK中,∵∠BDK=30°,BK=BE+EK=3$\sqrt{2}$+$\sqrt{6}$,
∴BD=BK÷cos30°=2$\sqrt{6}$+2$\sqrt{2}$,
∴DP=BD-PB=2$\sqrt{2}$,
∵∠CPD=∠PBC+∠NCM=30°+15°=45°,
∴DF=DP•sin45°=2$\sqrt{2}$$•\frac{\sqrt{2}}{2}$=2.
点评 本题考查圆综合题、等边三角形的判定和性质、垂径定理、等腰直角三角形的判定和性质、直角三角形30度角性质、角平分线的判定定理以及性质定理等知识,解题的关键是学会添加常用辅助线,熟练应用角平分线的判定定理以及性质定理,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
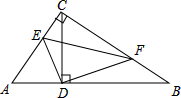 在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.
在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E,F分别是AC,BC边上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com