
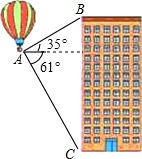
 热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80)
热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80) 分析 如图,过点A作AD⊥BC,垂足为D,根据题意,∠BAD=35°,∠CAD=61°,BC=300m,在Rt△ABD中,根据三角函数的定义得到BD=AD•tan35°,在Rt△AC中,根据三角函数的定义得到CD=AD•tan61°,于是得到结论.
解答 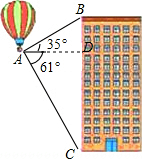 解:如图,过点A作AD⊥BC,垂足为D,
解:如图,过点A作AD⊥BC,垂足为D,
根据题意,∠BAD=35°,∠CAD=61°,BC=300m,
∵在Rt△ABD中,tan∠BAD=$\frac{BD}{AD}$,
∴BD=AD•tan35°,
∵在Rt△AC中,tan∠CAD=$\frac{CD}{AD}$,
∴CD=AD•tan61°,
又∵BC=BD+CD,
∴AD=$\frac{300}{tan35°+tan61°}$,
∴CD=AD•tan61°=$\frac{300•tan61°}{tan35°+tan61°}$≈$\frac{300×1.8}{0.7+1.8}$=216m,
答:热气球所在位置距地面的距离约为216m.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数求解.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
 已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (0,3) | C. | (-1,3) | D. | (-3,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.
甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
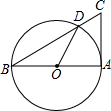 如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )| A. | 70° | B. | 35° | C. | 20° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com