
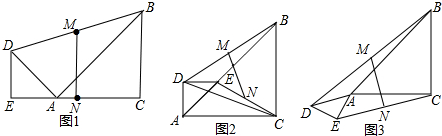
分析 (1)先判断出MN是△BDG的中位线,再判断出△EDN≌△CGN,得出结论进而判断出△CAE≌△BCG(SAS),即可得出结论;
(2)先求出DE,再判断出△DEM≌△BFM,最后用勾股定理求出FC,再用三角形的中位线即可;
(3)先判断出△EDN≌△CGN(SAS),再得出△CAE≌△BCG(SAS),即可.
解答 解:(1)MN⊥EC,且EC=2MN;
理由:如图1,延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,
∵M为BD中点,
∴MN是△BDG的中位线
∴BG=2MN,
在△EDN和△CGN中,
$\left\{\begin{array}{l}{DN=NG}\\{∠DNE=∠GNC}\\{EN=NC}\end{array}\right.$,
∴△EDN≌△CGN(SAS),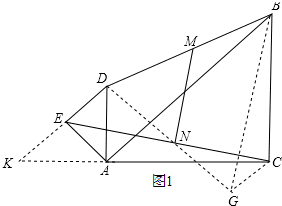
∴DE=CG=AE,∠GCN=∠DEN,
∴DE∥CG,
∴∠KCG=∠CKE,
∵∠EAK=45°,
∴∠CAE=180°-45°=135°
∴∠CKE=∠KCG=45°,
∴∠KCG=∠CKE=45°
∴∠BCG=90°+45°=135°,
∴∠CAE=∠BCG,
在△CAE和△BCG中,$\left\{\begin{array}{l}{AC=BC}\\{∠CAE=∠BCG}\\{AE=CG}\end{array}\right.$
∴△CAE≌△BCG(SAS),
∴BG=CE,
∵BG=2MN,
∴CE=2MN.
∵△CAE≌△BCG,
∴∠ECK=∠CBG,
∵∠ACB=∠ECK+∠BCE=90°,
∴∠CBG+∠BCE=90°,
∴∠BFC=90°,
∴BG⊥EC,
∵MN∥BG,
∴MN⊥EC;
(2)如图2,
在等腰Rt△ABC中,AB=$\sqrt{6}$,
∴BC=$\sqrt{3}$,
由旋转知,∠AED=∠EAC=90°,
∴DE∥AC,
∵∠BAC=45°,
∴∠EAD=45°,
∴DE=AD=1
连接EM并延长至F使EM=FM,连接CF,
∵EN=CN,
∴MN=$\frac{1}{2}$CF,
在△DEM和△BFM中,$\left\{\begin{array}{l}{DM=BM}\\{∠DME=∠BMF}\\{EM=FM}\end{array}\right.$,
∴△DEM≌△BFM,
∴BF=DE=1,∠MDE=∠MBF,
∴DE∥BF,
∴AC∥BF,
∴∠CBF=90°,
在Rt△BCF中,根据勾股定理得,CF=$\sqrt{B{F}^{2}+B{C}^{2}}$=2,
∴MN=$\frac{1}{2}$CF=1.
(3)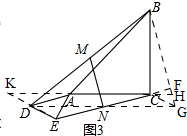 MN⊥EC,且EC=2MN;
MN⊥EC,且EC=2MN;
理由:如图3,延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,连接BG,延长EC交BG于F,延长AC交BG于H;
∵M为BD中点,
∴MN是△BDG的中位线
∴BG=2MN,
在△EDN和△CGN中,
$\left\{\begin{array}{l}{DN=NG}\\{∠DNE=∠GNC}\\{EN=NC}\end{array}\right.$,
∴△EDN≌△CGN(SAS)
∴DE=CG=AE,∠GCN=∠DEN,
∴DE∥CG,
∴∠CKE=∠KCG=∠HCG,
∴∠CAE=∠AED+∠CKE=90°+∠CKE=90°+∠HCG,
∵∠BCG=∠BCH+∠HCK=90°+∠HCG,
∠BCG=90°+45°=135°,
∴∠CAE=∠BCG,
在△CAE和△BCG中,$\left\{\begin{array}{l}{AC=BC}\\{∠CAE=∠BCG}\\{AE=CG}\end{array}\right.$
∴△CAE≌△BCG(SAS),
∴BG=CE,
∵BG=2MN,
∴CE=2MN.
∵△CAE≌△BCG,
∴∠ECK=∠CBG,
∵∠ACB=∠ECK+∠BCE=90°,
∴∠CBG+∠BCE=90°,
∴∠BFC=90°,
∴BG⊥EC,
∵MN∥BG,
∴MN⊥EC;
即:MN⊥EC,CE=2MN;
点评 此题是几何变换综合题,主要考查了全等三角形的性质和判定,勾股定理,三角形的中位线,解本题的关键是△EDN≌△CGN(SAS)和△CAE≌△BCG(SAS),作出辅助线是解本题的难点.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2007 | B. | 2008 | C. | 2009 | D. | 2010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
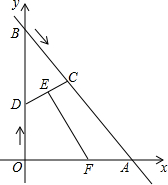 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO-OA-AC交于点F,设运动时间为t秒.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,点C从点B出发,以每秒5个单位长度的速度向点A匀速运动;同时点D从点O出发,以每秒4个单位长度的速度向点B匀速运动,到达终点后运动立即停止.连接CD,取CD的中点E,过点E作EF⊥CD,与折线DO-OA-AC交于点F,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 方程 | 方程的根x1、x2 |
| x2-5x+6=0 | x1=2,x2=3 |
| 6x2-5x+1=0 | x1=$\frac{1}{2}$,x2=$\frac{1}{3}$ |
| x2-7x+10=0 | x1=2,x2=5 |
| 10x2-7x+1=0 | x1=$\frac{1}{2}$,x2=$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com