
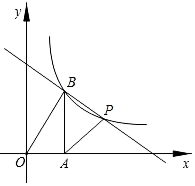
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
【答案】(1)k=12;B(2,6);(2)y=﹣![]() x+9;(3)0<x<2或x>4.
x+9;(3)0<x<2或x>4.
【解析】
(1)把P(4,3)代入y=![]() ,即可求出k的值;由S△AOB=S△PAB可求出点B的横坐标,代入反比例函数解析式可求出点B的坐标;
,即可求出k的值;由S△AOB=S△PAB可求出点B的横坐标,代入反比例函数解析式可求出点B的坐标;
(2)设直线BP的解析式为y=ax+b,将B(2,6),P(4,3)代入,利用待定系数法即可求出直线BP的解析式;
(3)根据图像直接写出结论即可.
(1)将P(4,3)代入函数y=![]() ,得:k=4×3=12,
,得:k=4×3=12,
∴反比例函数为y=![]() ,
,
∵△AOB和△PAB都可以看作以AB为底,它们的面积相等,
∴它们的底AB边上的高也相等,即点O和点P到直线AB的距离相等,
∴xP=2xB,
∵P(4,3),即xP=4,
∴xB=2,
代入y=![]() ,得:y=6,
,得:y=6,
∴B(2,6);
(2)设直线BP的解析式为y=ax+b,
分别代入B(2,6)、P(4,3),
得:![]() ,
,
解得![]() ,
,
∴直线BP的解析式为y=﹣![]() x+9;
x+9;
(3)在第一象限内,反比例函数大于一次函数的x的取值范围是0<x<2或x>4,
故答案为:0<x<2或x>4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知a=3,b和c是关于x的方程x2+mx+2-![]() m=0的两个实数根.
m=0的两个实数根.
(1)求△ABC的周长.
(2)求△ABC的三边均为整数时的外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向 A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二: 同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受 9 折优惠的概率为_______;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
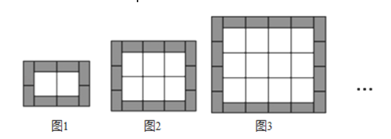
【题目】如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.
(1)问:依据规律在第6个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(2)某新学校教室要装修,每间教室面积为68m2 , 准备定制边长为0.5米的正方形白色瓷砖和长为0.5米、宽为0.25米的长方形黑色瓷砖来铺地面.按照此图案方式进行装修,瓷砖无须切割,恰好完成铺设.已知白色瓷砖每块20元,黑色瓷砖每块10元,请问每间教室瓷砖共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=﹣![]() ,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )
,下列结论:①图象必经过点(﹣3,1);②图象在第二,四象限内;③y随x的增大而增大;④当x>﹣1时,y>3.其中错误的结论有( )
A. ①④ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
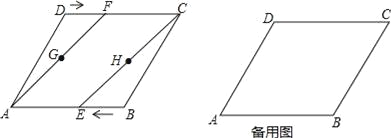
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
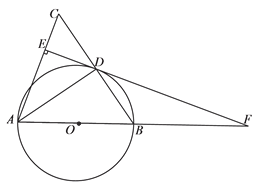
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线.
(2)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点(含端点
上的动点(含端点![]() ,
,![]() ),连结
),连结![]() ,以
,以![]() 所在直线为对称轴作点
所在直线为对称轴作点![]() 的对称点
的对称点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点,连结
的中点,连结![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(3)以![]() 其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
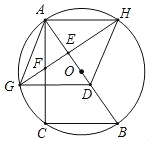
【题目】如图,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,交AC边于点F,交以AB为直径的⊙O于G,H,设BC=x.
(1)求证:四边形AGDH为菱形;
(2)若EF=y,求y关于x的函数关系式;
(3)连结OF,CG.
①若△AOF为等腰三角形,求⊙O的面积;
②若BC=3,则![]() CG+9=______.(直接写出答案).
CG+9=______.(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com