
【题目】如图,![]() 中,
中,![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,
分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2 cm/s.当点N第一次到达B点时,![]() 、
、![]() 同时停止运动.
同时停止运动.
(1)点![]() 、
、![]() 运动几秒时,
运动几秒时,![]() 、
、![]() 两点重合?
两点重合?
(2)点![]() 、
、![]() 运动几秒时,可得到等边三角形
运动几秒时,可得到等边三角形![]() ?
?
(3)当点![]() 、
、![]() 在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时
在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时![]() 、
、![]() 运动的时间.
运动的时间.
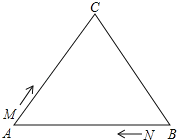
【答案】(1)12;(2)4;(3)能,此时M、N运动的时间为16秒.
【解析】
(1)首先设点M、N运动x秒后,M、N两点重合,表示出M,N的运动路程,N的运动路程比M的运动路程多12cm,列出方程求解即可;
(2)根据题意设点M、N运动t秒后,可得到等边三角形△AMN,然后表示出AM,AN的长,由于∠A等于60°,所以只要AM=AN,三角形ANM就是等边三角形;
(3)首先假设△AMN是等腰三角形,可证出△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB,NM的长,列出方程,可解出未知数的值.
(1)设点M、N运动x秒时,M、N两点重合,
x×1+12=2x,
解得:x=12;
(2)设点M、N运动t秒时,可得到等边三角形△AMN,如图①,
AM=t×1=t,AN=AB﹣BN=12﹣2t.
∵三角形△AMN是等边三角形,∴t=12﹣2t,
解得:t=4,∴点M、N运动4秒时,可得到等边三角形△AMN.
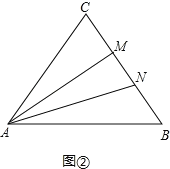
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由(1)知12秒时M、N两点重合,恰好在C处,
如图②,假设△AMN是等腰三角形,∴AN=AM,∴∠AMN=∠ANM,∴∠AMC=∠ANB.
∵AB=BC=AC,∴△ACB是等边三角形,∴∠C=∠B,
在△ACM和△ABN中,
∵ ,∴△ACM≌△ABN,∴CM=BN,
,∴△ACM≌△ABN,∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,∴CM=y﹣12,NB=36﹣2y,CM=NB,
y﹣12=36﹣2y,
解得:y=16.故假设成立,∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.



 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N.AH⊥MN于点H.
(1)当∠MAN绕点A旋转到BM=DN时,请你直接写出线段AH与AB的数量关系______.(不需证明)
(2)当∠MAN绕点A旋转到BM≠DN时,问(1)中线段AH与AB的数量关系还成立吗?若成立,给出证明,若不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
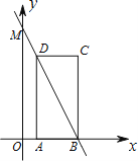
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(![]() ,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
(1)求直线y=kx+b(k≠0)的表达式;
(2)若直线y=kx+b(k≠0)与y轴交于点M,求△CBM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=40°,则∠CDE的度数为( )
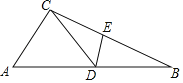
A.50°B.40°C.60°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC经过一定的运动得到△A1B1C1,然后以点A1为位似中心将△A1B1C1放大为原来的2倍得到△A1B2C2,如果△ABC上的点P的坐标为(a,b),那么这个点在△A1B2C2中的对应点P2的坐标为 ( )
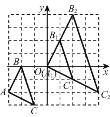
A. (a+3,b+2) B. (a+2,b+3)
C. (2a+6,2b+4) D. (2a+4,2b+6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,点C是OA的中点,过点C作CD⊥OA于C交一次函数图象于点D,P是OB上一动点,则PC+PD的最小值为( )

A.4B.![]() C.2
C.2![]() D.2
D.2![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
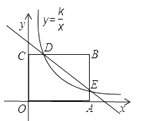
【题目】如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=![]() 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及E点的坐标;
(2)求直线DE的解析式;
(3)若矩形OABC对角线的交点为F (2,![]() ),作FG⊥x轴交直线DE于点G.
),作FG⊥x轴交直线DE于点G.
①请判断点F是否在此反比例函数y=![]() 的图象上,并说明理由;
的图象上,并说明理由;
②求FG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com