
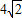 ,求BC的长.
,求BC的长.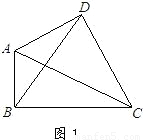

 解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;
解:(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;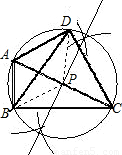
 AC.
AC. AC,
AC, AC为半径的同一个圆上;
AC为半径的同一个圆上;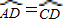 ,
,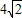 ,
, AB×h=2AB=6,
AB×h=2AB=6, AB×BC=
AB×BC= BC,
BC, BC×h=2BC,S△ACD=
BC×h=2BC,S△ACD= S正方形ACEF=
S正方形ACEF= AC2=
AC2= (BC2+9),
(BC2+9), BC+
BC+ (BC2+9)=6+2BC
(BC2+9)=6+2BC

 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
 标.
标.查看答案和解析>>
科目:初中数学 来源: 题型:
 21、定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.(1)如图,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段
21、定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.(1)如图,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |


查看答案和解析>>
科目:初中数学 来源: 题型:
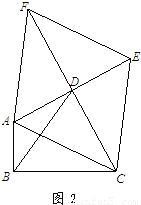
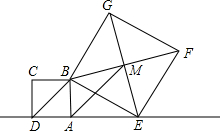 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.查看答案和解析>>
科目:初中数学 来源:2013届江苏扬州江都区麾村中学九年级上学期期中考试数学试卷(带解析) 题型:解答题
如图1,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是 轴正半轴上一动点(OD>1),连结BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交
轴正半轴上一动点(OD>1),连结BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交 轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图2中,过点M作MG⊥ 轴于点G,连结DN,若四边形DMGN为损矩形,求D点坐标.
轴于点G,连结DN,若四边形DMGN为损矩形,求D点坐标. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com