
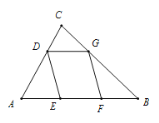
【题目】如图,在![]() 中,
中,![]() ,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】聪明好学的亮亮看到一课外书上有个重要补充:
(角平分线定理)三角形一个内角的平分线分对边所成的两条线段与这个角的两邻边对应成比例.于是他就和其他同学研究一番,写出了已知、求证如下:
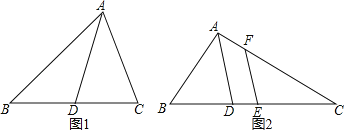
“已知:如图1,△ABC中,AD平分∠BAC交BC于点D,求证:![]() ”
”
可是他们依然找不到证明的方法,于是,老师提示:过点B作BE∥AC交AD延长线于点E,于是得到△BDE∽△CDA,从而打开思路.
(Ⅰ)请你按老师的提示或你认为其他可行的方法帮亮亮完成证明.
(Ⅱ)利用角平分线定理解决如下问题:
如图2,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F,AB=7,AC=15,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.

(1) 求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2) 连接OA,OC.求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
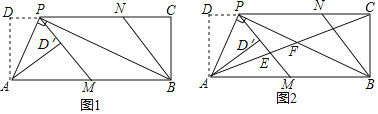
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
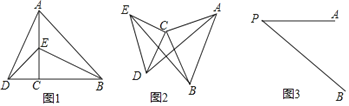
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边CD上(不与点C,D重合),连接AE,BD交于点F.
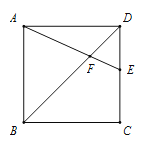
(1)若点E为CD中点,AB=2![]() ,求AF的长.
,求AF的长.
(2)若![]() ∠AFB=2,求
∠AFB=2,求![]() 的值.
的值.
(3)若点G在线段BF上,且GF=2BG,连接AG,CG,设![]() =x,四边形AGCE的面积为
=x,四边形AGCE的面积为![]() ,
,![]() ABG的面积为
ABG的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点![]() ,
,![]() ,
,![]() .
.

(1)求抛物线的解析式和对称轴;
(2)![]() 是抛物线对称轴上的一点,求满足
是抛物线对称轴上的一点,求满足![]() 的值为最小的点
的值为最小的点![]() 坐标(请在图1中探索);
坐标(请在图1中探索);
(3)在第四象限的抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是以
是以![]() 为对角线且面积为
为对角线且面积为![]() 的平行四边形?若存在,请求出点
的平行四边形?若存在,请求出点![]() 坐标,若不存在请说明理由.(请在图2中探索)
坐标,若不存在请说明理由.(请在图2中探索)
查看答案和解析>>
科目:初中数学 来源: 题型:
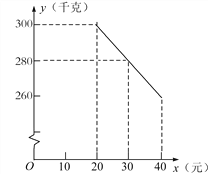
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
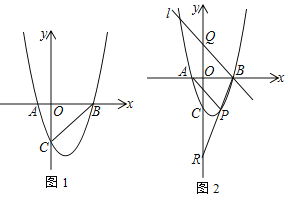
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣2x﹣3a与x轴交于A、B两点,与y轴交于C点,OC=OB,点P为抛物线上一动点
(1)求抛物线的解析式;
(2)当点P运动到抛物线对称轴右侧时如图2,连PC、BC、BP得△BCP.设△BCP的面积为s,点P的横坐标为x.若s<![]() ,求x的取值范围;
,求x的取值范围;
(3)当点P运动到第四象限时,连AP、BP,BP交y轴于点R,过B作直线l∥AP交y轴于点Q,问:QR、OC之间是否存在确定的数量关系?若存在,请求出并证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com